Jaime Villamil*

Enviar los comentarios al correo: jaime_villamil@yahoo.com . Artículo recibido el 24 de noviembre de 2005, aprobada su publicación el 1 de junio de 2006.

Resumen

El clásico modelo de valoración de opciones europeas de Black y Scholes (1973) supone que los retornos logarítmicos de un activo financiero se distribuyen normalmente, no obstante varios estudios empíricos muestran, primero, que esta distribución puede ser asimétrica y tener “colas pesadas” y, segundo, que la varianza del precio del activo no es finita. Este artículo presenta la implementación numérica de tres modelos alternativos: elasticidad constante de la varianza (1976), jump-diffusion (1976) y volatilidad estocástica (1987).

Palabras claves: ecuaciones diferenciales estocásticas, lema de Itô, valoración de opciones, simulación de Monte Carlo. JEL: C15, C63, G13.

Abstract

Black and Scholes' (1973) classic model of valuation of European options assumes that the logarithmic returns of a financial asset are distributed normally, even though several empirical studies show, first, that this distribution may be asymmetric and have “heavy tails”, and second, that the variance of the price of the asset is not finite. This article presents the numerical implementation of three alternative models: constant elasticity of variance (1976), jump-diffusion (1976), and stochastic volatility (1987).

Key words: stochastic differential equations, Itô’s lemma, valuation of options, Monte Carlo simulation. JEL: C15, C63, G13.

Résumé

Le modèle classique d´évaluation des options européennes de Black et Scholes (1973) suppose que les retours logarithmiques d´un actif financier se distribuent normalement, cependant plusieurs études empiriques montrent, tout d´abord, que cette distribution peut être asymétrique et avoir « des queues lourdes » et, ensuite, que la variance du prix de l´actif n´est pas finie. Cet article présente la mise en application numérique de trois modèles alternatifs : l´élasticité constante de la variance (1976), jump-diffusion (1976) et la volatilité stochastique (1987).

Mots clés : équations différentielles stochastiques, devise de Itô, évaluation d´options, simulation de Monte Carlo. JEL: C15, C63, G13.

En 1969 Black y Scholes ya habían concebido la hoy famosa ecuación para determinar el precio “justo” (de no arbitraje) que un inversionista debe pagar por el derecho a comprar o vender un activo financiero (con unas características particulares) en un tiempo pactado previamente. El artículo fue rechazado en dos revistas importantes: Journal of Political Economy y Review of Economics . Sólo hasta 1973, después de realizar unas modificaciones por sugerencia de Merton Miller y Eugene Fama, fue publicado en la primera de las revistas mencionadas.

Una de las implicaciones de la hipótesis de los mercados eficientes formulada por E. Fama (1969) es que ningún especulador en promedio podría ganar sistemáticamente más que el mercado. En otras palabras, estos mercados no son predecibles. Esta conclusión se puede confirmar empíricamente cuando se ajustan modelos propuestos por la teoría de las series de tiempo lineales a las variables financieras. En el caso de tipos de cambio, con mayor frecuencia, se muestra que el paseo aleatorio es el que mejor logra explicar los datos. Esto quiere decir que el valor futuro del precio de un activo no guarda relación lineal con su historia, por esta razón el conocimiento del comportamiento en el pasado no aporta información para dilucidar su comportamiento en el futuro. Algunos autores han buscado en teorías más complejas resultados que contradigan dicha hipótesis: la teoría del caos admite que el aparente comportamiento volátil de una variable puede ser generado por una ecuación en diferencias o diferencial determinística, las series de tiempo no lineales buscan una relación no lineal específica (Tong 1990) y las redes neuronales (que simulan las neuronas biológicas y sus conexiones mediante funciones de activación no lineales como la función logística y la tangente hiperbólica) dan lugar a relaciones altamente no-lineales entre unas variables explicativas y otras explicadas. El primer trabajo que aplicó redes neuronales a temas financieros fue el de White (1988).

Si se acepta la hipótesis de los mercados eficientes se debe aceptar también al paseo aleatorio (en tiempo discreto) y al movimiento browniano (en tiempo continuo) como los “mejores” modelos para explicar el comportamiento de las variables financieras, esto pese a que no son útiles para fines predictivos. Bachelier (1900) fue el primero en incorporar el movimiento browniano o proceso Gauss-Wiener estándar como explicación del comportamiento de las variables financieras, esta propuesta falló porque este proceso estocástico permitía valores negativos para los precios de los activos financieros. Mucho tiempo después Black, Scholes y Merton asumieron como proceso estocástico el movimiento browniano geométrico que eliminaba esa desventaja.

En el principal planteamiento de valoración de opciones en tiempo discreto (el árbol binomial) también está presente la idea de Fama. En este modelo Cox, Ross y Rubinstein (1979) asumen que en un período el precio de un activo se puede incrementar en un factor µ con probabilidad p y decrecer en d con probabilidad 1 - p y así sucesivamente para varios períodos Δt en los que se particione el intervalo de tiempo que existe desde la firma del contrato hasta el vencimiento [t, T]. Este artículo presentó la fórmula de Black-Scholes como un caso límite del árbol binomial cuando el valor Δt se hace infinitamente pequeño.

ANÁLISIS DE BLACK - SCHOLES

El supuesto más importante de estos autores es que el comportamiento del precio de un activo sigue un movimiento browniano geométrico (MBG). Para entenderlo es preciso conocer las propiedades del llamado movimiento browniano o proceso Gauss-Wiener estándar.

Definición 1: se dice que el proceso estocástico [W_t , t > 0 ]. con respecto a la filtración t es un proceso Gauss-Wiener si cumple ¹:

• W₀ = 0con probabilidad uno

• [ W_t - W_s] − N(O, t - s)

• Las variables aleatorias [ W_t - W_s] y [ W_v - W_µ] son i.i.d νS < t < µ < v (incrementos independientes)

• [W_t+s - W_s] ^d = W_t (incrementos estacionarios)

• Las trayectorias de W_t son continuas con probabilidad uno

El análisis que hacen Black y Scholes (1973) se sostiene en las siguientes hipótesis: (a) no hay costos de transacción, (b) los precios se forman continuamente, (c) no hay restricciones a la venta en corto ², (d) las tasas de captación y de colocación de recursos en una economía son iguales y se usa como proxy de la tasa de rendimiento de un activo libre de riesgo, esta tasa se supone conocida y constante, (e) el activo subyacente a los derivados financieros no paga dividendos, (f) el MGB es el proceso que se asume rige el precio del activo, y (g) la opción sólo puede ser ejercida al vencimiento, es decir, trata únicamente con opciones europeas ³.

El análisis de Black y Scholes considera un bono B como activo libre de riesgo y la evolución su precio, con base en el supuesto (d), se representa por medio de un proceso determinístico:

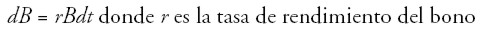[ 1]

Resolviendo la ecuación diferencial ordinaria [ 1] se tiene una ecuación de comportamiento determinística:

[ 2]

Si S_t el precio del subyacente en el tiempo t, según el supuesto (f), este se representa por la expresión:

[ 3]

Donde µ es el retorno logarítmico esperado, σ la desviación estándar de los retornos logarítmicos de S_t y W es un proceso Gauss-Wiener. La ecuación diferencial estocástica [ 3] describe el comportamiento de una variable que sigue un movimiento browniano geométrico ⁴.

Las expresiones [ 2] y [ 3] deben ser evaluadas en el intervalo [t, T] que indica el tiempo hasta el vencimiento de contrato (T) a partir de su firma en un tiempo (t).

Definición 2 (Lema de Itô): sea un proceso estocástico X_t que satisface dX = µ(X, t)dt + σ(X, t)dW y f (X, t) una función no aleatoria con derivadas parciales continuas, entonces la variable Y_t = f (X, t) sigue un proceso estocástico que viene dado por:

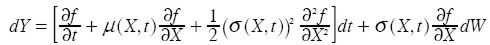[ 4]

Si se supone la función Y_t = ln(S_t) y se aplica el Lema de Itô para resolver la EDE [ 3] se tiene:

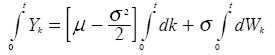[ 5]

Integrado [ 5] se sigue:

[ 6]

Resolviendo ⁵:

[ 7]

Se sabe que la función de pago de una opción call europea en cualquier momento antes del vencimiento (T - t) es C(S_t , T - t) = Max(S_t - E, 0) y de una opción put europea es P(S_t , T - t) = Max(E - S_t , 0) donde E es el strike o precio de ejercicio de la opción. El interés fundamental del análisis de Black y Scholes es encontrar una función C (•) el caso de la opción call (o una función P (•) en el caso de la opción put) que indique el precio de no-arbitraje del derivado dado que S_t sigue el comportamiento descrito en [ 7] .

Aplicando el Lema de Itô a la EDE [ 3] suponiendo que C (•) es una función con derivadas parciales continuas (el análisis para encontrar P(•) es similar) se tiene que:

[ 8]

Black y Scholes construyen un portafolio que consiste en Δ unidades del activo libre de riesgo y de β unidades de la opción call:

[ 9]

Derivando [ 9] se obtiene:

[ 10]

Reemplazando [ 3] y [ 8] en [ 10] se consigue:

[ 11]

Black y Scholes eliminan el término aleatorio (el segundo del lado derecho) haciendo:

[ 12]

Reemplazando [ 12] en [ 11] se tiene:

[ 13]

Black y Scholes usan el siguiente argumento: en una valoración de riesgo neutral este portafolio debe obtener los mismos rendimientos que el activo libre de riesgo (el bono), esto es, el portafolio P debe seguir un proceso semejante al de la ecuación [ 1] :

[ 14]

Igualando [ 13] y [ 14] :

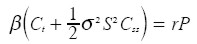[ 15]

Reemplazando [ 9] en [ 15] .

[ 16]

Dado que se eliminó la aleatoriedad mediante el uso de [ 12] :

[ 17]

Reorganizando términos:

[ 18]

La expresión [ 18] es conocida como la ecuación diferencial parcial de Black y Scholes, su solución sujeta a las condiciones de frontera C(S, 0) = max(S_T - E, 0) y C(0, T - t) ofrece una expresión directa para el cálculo de la prima o precio de la opción call, esta solución puede obtenerse mediante Series de Fourier o por medio del método de solución por similaridades expuesto en Almgren (1998) y en Wilmott et al . (1995, 76). La conocida fórmula de Black y Scholes [ 19] es la solución a la ecuación [ 18] ⁶:

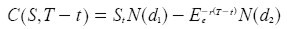[ 19]

Donde: N(•) es la función de distribución acumulada de la normal estándar:

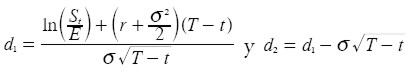Posterior a la publicación del artículo de Black y Scholes en 1973 surgió la controversia con relación a que los retornos de los derivados financieros no son normalmente distribuidos como se deduce de suponer el MBG como proceso del precio de los activos financieros. Varios estudios empíricos demostraron que la distribución de los retornos no tenía una distribución normal sino una distribución asimétrica, que termina con “colas pesadas”. De otro lado también se mostró que la varianza de los precios no era finita. Los modelos de elasticidad constante de varianza (CEV su sigla en inglés) y Jump diffusion (ambos de 1976) buscaron una explicación a la primera inquietud, entre tanto que el modelo de volatilidad estocástica (1987) consideró el segundo aspecto.

APLICACIÓN DE LA FÓRMULA DE BLACK Y SCHOLES

Para ilustrar el uso de la expresión [ 19] se supone una opción call europea sobre el tipo de cambio EUR/USD. Se toma como valor actual (en t) la cotización en el día 03 de Enero del año 2005 a las 10 horas de Londres (S_t = 1,3533), como precio strike E = 1,3533, aunque estos vencimientos no existen en la práctica se asume un día T = 1, se supone un diferencial anual entre las tasas libre de riesgo de Estados Unidos y de la Comunidad Europea de 2% que llevado a valor diario es igual a r = 0,072%. El parámetro más difícil de precisar es la volatilidad del activo. Tres formas de estimarlo son: la desviación estándar de los retornos logarítmicos del registro histórico del precio del activo, la varianza incondicional obtenida mediante los modelos GARCH(p, q) y la volatilidad implícita, usando el precio de la call europea dado por el mercado y despejando el valor de σ de la ecuación [ 19] . Usando un AR(1) para el nivel de la variable y un GARCH(1, 1) con una serie diaria de los retornos logarítmicos del mes de diciembre de 2004 se estimó un valor de volatilidad diaria σ = 0,77% ⁷.

Con los anteriores parámetros se creó el siguiente código en Matlab 6.5 para valorar la opción call europea, el resultado es 0,0046608 que corresponde con el valor (en dólares) de no arbitraje que debe pagarse por ejercer el derecho a comprar Euros al precio USD 1,3533 el día 4 de enero de 2005 a las 10 horas de Londres.

SIMULACIÓN DE MONTE CARLO

La simulación de Monte Carlo consiste en generar varias trayectorias con base en algún proceso estocástico del precio de un activo financiero. Para un proceso particular de S_t, la simulación encuentra varios valores de S_t [ del precio del activo en la fecha de vencimiento del contrato). Para cada valor de S_t se calcula el pago de la opción, se estima un valor medio de esta variable aleatoria y se trae a valor presente usando como tasa de descuento la tasa libre de riesgo. El precio de la opción estimado θ˜ viene dado por la expresión [ 20] :

[ 20]

Donde m es el número de simulaciones. Si se supone que el proceso del precio se rige por la EDE dX = µ(X, t)dt + σ(X, t)dW, la simulación de Monte Carlo para encontrar el valor puede basarse en la solución analítica de la EDE si esta existe o en la solución numérica si no existe. Por ejemplo, si se asume el MBG como proceso del precio, la simulación debe originarse a partir de la expresión [ 7] que es la solución analítica de [ 3] , pero si encontrar dicha solución fuera imposible se debe poner la expresión [ 3] en términos discretos para aproximar el valor S_T de cada trayectoria.

El resultado de la simulación de Monte Carlo se acostumbra a presentar en intervalos de confianza a un nivel de confianza 1 - α.

[ 21]

Donde σ˜_θ es la varianza estimada de S_T y z_{1 - α/2} es el percentil de una distribución normal estándar.

Si MBG es el proceso asumido para el precio del activo, a medida que el número de simulaciones m sea mayor, el valor de la opción estimado θ˜ debe converger a la solución de la fórmula de Black Scholes dada por la expresión [ 19] en el caso de una call europea. Con la gráfica 1 se ilustra esta afirmación.

SOLUCIÓN NUMÉRICA DE UNA EDE

Con frecuencia la solución de las EDE asumidas no tiene solución analítica, o si la tiene no se puede determinar la distribución teórica de S_T. En ambos casos se necesita hallar una solución numérica de la EDE . El método numérico usado para encontrar esta solución es conocido como Euler-Maruyama y es similar al método de Euler para resolver ecuaciones diferenciales ordinarias.

Sea una variable X_t para la que se asume el proceso dado por la EDE [ 22] : con W_t un proceso de Gauss-Wiener:

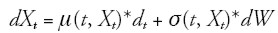[ 22]

Se define el tamaño de paso h = T/n con n siendo el número de períodos en que se divide el intervalo [0, T ] de tal modo que t_i = t₀ + ih. La solución numérica para X_t utilizando el método Euler-Maruyama viene dada por:

[ 23]

Para i = 1,2,..., n

Por la propiedad de incrementos estacionarios del movimiento browniano se tiene que B_ih - B_{(1 - i)h} =^d B_h y se sabe que B_h ~ N(O , h) = √h * N(O, 1) luego el método iterativo de Euler- Maruyama puede escribirse como:

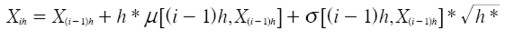[ 24]

Donde ξ ~ N(O, 1)

A medida que el valor de h sea más pequeño la aproximación de la solución numérica es más exacta, esto a expensas de un mayor costo computacional.

MODELO CEV

El modelo CEV (siglas en inglés de elasticidad constante de varianza) fue propuesto originalmente por Cox y Ross (1976). Este se muestra en la expresión [ 25] . Un valor de α estrictamente menor que uno indica que cuando el precio del stock aumenta la volatilidad decrece. Por el contrario, para valores mayores que uno, señala que cuando el precio del stock aumenta la volatilidad también. Un ejemplo de este aspecto es el cambio de tendencia de la cotización del EUR/USD el 31 de diciembre de 2004, que pasó de lograr el máximo histórico de 1,3655 a un descenso persistente acompañado de una alta volatilidad debido al comportamiento en manada de inversionistas y especuladores que mantenían posiciones largas y que se vieron obligados a liquidarlas para disminuir sus pérdidas ⁸.

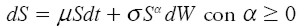[ 25]

Observar que para α = 1 se tiene el caso del MBG usado por Black-Scholes. Con el fin de comparar el resultado de Black-Scholes de la ecuación [ 19] con la simulación de Monte Carlo de la EDE [ 25] , el cuadro 1 muestra la estimación del precio de la call europea con base en la simulación de 10.000 posibles caminatas del precio del activo y la solución numérica de [ 25] con h =1/24. A continuación se presenta el código del procedimiento en Matlab.

Del cuadro 1 se puede concluir que en la medida que la constante α crece el valor de la prima es más costoso. Este hecho se puede interpretar del siguiente modo: si la varianza responde más que proporcionalmente al cambio del precio de un activo, la incertidumbre (volatilidad) será mayor, y la prima que se deba pagar por poseer el derecho a comprar o vender será igualmente más costosa .

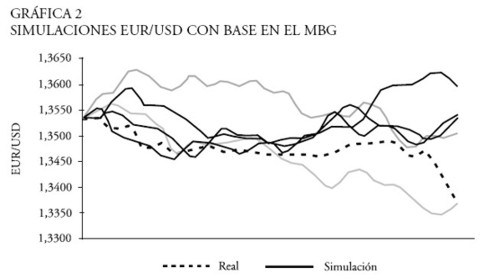
En la gráfica 2, para el caso particular α = 1 (MBG), se dibujan cinco caminos posibles y se comparan con los valores realizados (frecuencia horaria) entre el 3 y 4 de enero de 2005 a las 10 horas de Londres.

MODELO JUMP DIFFUSION

El modelo de Merton (1976) asume como comportamiento del precio del activo el proceso de la EDE [ 26] . Con esta expresión se desea explicar por qué la distribución de los retornos logarítmicos de un activo financieros puede tener “colas pesadas”. Este tipo de distribuciones se presenta debido a que las trayectorias continuas asumidas por el MBG pueden ser repentinamente perturbadas por grandes caídas o saltos conocidos en los mercados como “crash”. Estas caídas se producen como respuesta a un anuncio en los mercados, para el caso del EUR/USD la cotización es muy sensible a la publicación oficial de las cifras de desempleo, crecimiento económico, déficit fiscal y tasas de interés ya sea por parte de la FED para la economía americana o del Banco Central Europeo para la Comunidad Europea.

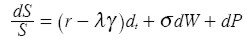[ 26]

Donde S: precio del activo, r: tasa de interés libre de riesgo, λ: número promedio de saltos por cada T, γ: porcentaje de cambio del activo, α: volatilidad (desviación estándar del retorno logarítmico del activo), W: proceso de Gauss-Wiener o movimiento browniano, P: proceso de Poisson; W y P son procesos estocásticos independientes.

Las caídas en el mercado en el modelo de Merton son representadas por un proceso de Poisson. Las variables aleatorias que registran el número de ocurrencia de un evento por unidad de tiempo, espacio, volumen o cualquier otro índice suelen asociarse con la distribución de Poisson. Algunas de estas variables, que también suelen llamarse de conteo, son: los accidentes de tránsito fatales por semana en una ciudad, el número de llamadas por hora que recibe un centro de atención telefónica, el número de organismos por unidad de volumen en un fluido, etc. En el caso de Merton (1976) la variable aleatoria es el número de caídas del precio de un activo financiero en el mercado por período de tiempo. La distribución de Poisson tiene la siguiente forma:

El parámetro λ es no negativo. Si una variable aleatoria Y esta distribución entonces su valor esperado y varianza son iguales a este parámetro. E[Y ] = Var[Y ] = λ. A λ se le conoce como tasa promedio de ocurrencia o en lenguaje epidemiológico como tasa de incidencia que hace referencia a la frecuencia con que ocurre un evento.

Siguiendo el análisis de Black-Scholes bajo el supuesto de que el precio del activo sigue el proceso dictado por la EDE [ 26] se llega a la expresión [ 27] ⁹:

[ 27]

Donde C_BS (S_t , T - t) es la valoración de la call por Black Scholes (BS) con los mismos parámetros excepto que la volatilidad se redefine como:

[ 28]

El cuadro 2 muestra el resultado de la valoración de una opción call europea para diferentes combinaciones de los parámetros  λ y γ. Abajo se presenta el código del modelo de Merton.

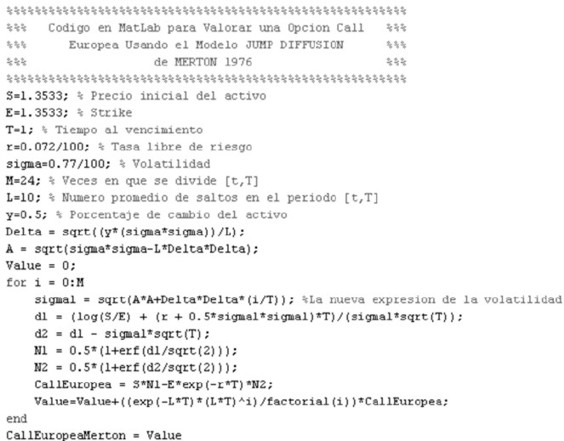MODELO DE VOLATILIDAD ESTOCÁSTICA

La varianza instantánea asumida en el modelo Black y Scholes es constante a través del tiempo, no obstante, en la misma lógica del modelo CEV pueden existir períodos de calma o de euforia en los mercados financieros que se traducen en menor o mayor varianzas de los retornos logarítmicos. Este modelo fue propuesto por Hull y White en 1987 ¹⁰. Se asumen dos EDE : una para el precio del activo (S) y otra para la varianza (V ):

[ 29]

[ 30]

Donde S_t: precio del activo en t, µ : retorno esperado del activo (se usa la tasa de interés libre de riesgo), V: varianza de los retornos logarítmicos del activo, a: constante de proporcionalidad con respecto a las diferencia instantánea de la varianza (V) respecto de la varianza incondicional de largo plazo (V₀ ), b: constante de proporcionalidad al término estocástico de la varianza, α: parámetro que mide la elasticidad de la varianza consigo misma (si el valor de α es mayor que uno quiere decir si en el período actual la varianza aumentó entonces en el siguiente período será más grande, para valores menores que uno significa lo contrario);   W₁ y W₂ son procesos de Gauss-Wiener independientes.

Para los valores a = b = 1 y α = 0.5 se tiene el proceso con reversión a la media de Ornstein-Uhlenbeck que en tiempo discreto corresponde al modelo GARCH(p, q).

En el cuadro 3 se muestra la estimación puntual del precio de la opción call europea por simulación de Monte Carlo usando la solución numérica Euler-Maruyama del sistema de ecuaciones [ 29] y [ 30] . Se simularon 10.000 trayectorias del precio del activo y para la solución numérica se consideró un tamaño de paso h = 1/24 . El código aparece debajo de cuadro 3.

CONCLUSIONES

Cuando se realiza la simulación de Monte Carlo asumiendo que el proceso de activo financiero es MBG se muestra que la convergencia del precio estimado del derivado a la solución de la fórmula Black y Scholes se logra con un número alto de simulaciones. Para el caso en el que no se puede obtener la solución analítica de la valoración de la opción, la precisión en el método de Monte Carlo puede ser mejorada combinando un número grande de simulaciones con un valor pequeño de tamaño de paso. La convergencia de la simulación a la solución analítica se convierte en una importante ventaja cuando se utilizan modelos con los que no se puede obtener dicha solución, o que cuando se obtiene no se puede encontrar la distribución teórica de los precios (o de la función de pago de la opción) al final de cada trayectoria.

Los modelos más realistas del comportamiento de los precios de los activos financieros que el movimiento browniano geométrico implícito en la fórmula de Black y Scholes (1973) reconocen la presencia de cambios de dirección repentinos en las trayectorias como respuesta a cualquier clase de noticia que modifique las expectativas de los inversionistas. La respuesta a este choque puede ser brusca para lo cual se emplea el modelo jump diffusion de Merton (1976). O puede traducirse en altas volatilidades que se prolongan por un tiempo mientras se regresa a condiciones normales, en esta situación se usa el modelo de elasticidad constante de varianza de Cox y Ross (1976) o el de volatilidad estocástica de Hull y White (1987). En conjunto estos modelos producen un valor de la opción más alto que el de Black y Scholes porque admiten la posibilidad de una volatilidad mayor sobre la posición final del precio del activo.

Se puede pensar en modelos más complejos, por ejemplo que combinen un proceso para el nivel del precio como el propuesto por Merton en la ecuación [ 26] con un proceso de varianza como en el modelo de volatilidad estocástica de la ecuación [ 30] dando lugar a complicados sistemas que probablemente no tengan una forma analítica de ser solucionados. Para estos modelos más sofisticados la simulación de Monte Carlo es una herramienta poderosa que permite implementarlos.

NOTAS AL PIE

1 En esta definición se asume que el espacio de probabilidad (Ω, , P) está dado.

2 Se dice que hay venta en corto cuando un inversionista vende un activo financiero que ha conseguido prestado de otro inversionista.

3 Una opción es un derecho –mas no una obligación– de comprar o vender un activo (con unas características predefinidas) en un tiempo futuro. Desde el punto de vista del ejercicio de dicho derecho, si el contrato establecido permite hacerlo efectivo sólo al vencimiento se habla de opción ‘europea’, si se ofrece la libertad de ejercerlo en cualquier momento desde la firma hasta el vencimiento se habla de opción ‘americana’.

4 A una expresión del tipo dX = µ(x, t)+ σ(X, t) dW donde µ (-) y σ (-) son funciones de valor real y W un proceso Gauss-Wiener se le conoce como ecuación diferencial estocástica (EDE). Su solución requiere de la aplicación del Lema de Itô.

5 Para la solución de la integral estocástica ∫ ₀^t dW_k ver Øksendal (1985, 21).

6 De forma similar para una opción put europea se tiene P (S, T - t) = E^{-r (T - t)} N (- d₂) - S_tN (-d₁) .

7 Se usó un proceso AR(1) por la fuerte evidencia que existe de que el comportamiento de la tasa EUR/USD es un paseo aleatorio.

8 Se dice que un inversionista tiene una posición larga si espera obtener un beneficio con la compra de un activo financiero.

9 De forma similar para la opción put europea .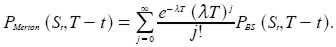

10 Heston (1993) propone una versión más completa de este modelo.

REFERENCIAS BIBLIOGRÁFICAS

1. Almgren, R. (1998) Solving the Black Scholes Equation , disponible en www.math.toronto.edu/almgren/finmath/pde-01/notes1.pdf         [ Links ]

2. Bachelier, L. (1900) “Théorie de la speculation”, Annales Scientifiques de l'È.N.S. , 3ª serie, tomo 17: 21-86.         [ Links ]

3. Black, F. y Scholes, M. (1973) “The pricing of options and corporate liabilities”, Journal of Political Economy , 81: 637-659.         [ Links ]

4. Cox, J. y Ross, S. (1976) “The valuation of options for alternative stochastic processes”, Journal of Financial Economics , 3: 145-166.         [ Links ]

5. Cox, J., Ross, S. y Rubinstein, M. (1979) “Option pricing: a simplified approach”, Journal of Financial Economics , 7: 229-264.         [ Links ]

6. Fama, Eugene (1969) “The behaviour of stock market prices”, Journal of Business , 38: 34-105.         [ Links ]

7. Forsyth, P. (2005) A Introduction to Computational Finance without Agonizing Pain , disponible en www.cs.uwaterloo.ca/~paforsyt/agon.pdf         [ Links ]

8. Glasserman, P. (2003) Monte Carlo Methods in Financial Engineering , Springer-Verlag.         [ Links ]

9. Heston, L. (1993) “A closed form solution for options with stochastic volatility with applications to bonds and currency options”, Review of Financial Studies , 6(2): 327-343.         [ Links ]

10. Higham, D. J. y Higham, N. J. (2000) Matlab Guide , Filadelfia : SIAM .         [ Links ]

11. Higham, D. J. (2001) “An algorithmic introduction to numerical simulation of stochastic differential equations”, SIAM Review , 43(3): 525-546.         [ Links ]

12. Hull , J. y White, A. (1987) “The pricing options on assets with stochastic volatilities”, Journal of Finance , 42(2): 281-300.         [ Links ]

13. Hull , J. (2003) Options, Futures and others Derivatives , Prentice Hall.         [ Links ]

14. Johnson, H. y Shanno, D. (1987) “Option pricing when the variance is changing”, Journal of Finance and Quantitative Analysis , 22(2): 143-151.         [ Links ]

15. Kloeden, P y Platen, E. (1992) Numerical Solution of Stochastic Differential Equations , Springer-Verlag.         [ Links ]

16. Merton, R. (1976) “Option pricing when underlying stock returns are discontinuous”, Journal of Financial Economics , 3: 125-144.         [ Links ]

17. Øksendal, B. (1985) Stochastic Differential Equations. An Introduction with Applications , Springer-Verlag, 5ª edición.         [ Links ]

18. Soren, S. y Neilsen, K. (editores) (2002) Programming Languages and Systems in Computational Economics and Finance , Kluwer.         [ Links ]

19. Tong, H. (1990) Non Linear Time Series , Clarendon Press Oxford .         [ Links ]

20. White, H. (1988) “Economic prediction using neural networks: the case of IBM daily stock returns”, Proc IEEE-ICNN , II: 451-458.         [ Links ]

21. Wilmott, P., Howison, S. y Dewynne, J. (1995) The Mathematics of Financial derivatives. A Student Introduction , Cambridge University Press.         [ Links ]