Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
DYNA
versão impressa ISSN 0012-7353versão On-line ISSN 2346-2183
Dyna rev.fac.nac.minas v.77 n.163 Medellín jul./set. 2010
MODELING OF DIRECT SOLAR RADIATION IN A COMPOUND PARABOLIC COLLECTOR (CPC) WITH THE RAY TRACING TECHNIQUE
MODELAMIENTO DE LA REFLEXIÓN SOLAR DIRECTA EN UN COLECTOR PARABÓLICO COMPUESTO (CPC) USANDO LA TÉCNICA DE “RAY-TRACING”
JOSÉ A. COLINA-MÁRQUEZ
Departamento de Ingeniería Química. Universidad de Cartagena, jcolinam@unicartagena.edu.co
ANDRÉS F. LÓPEZ-VÁSQUEZ
Chemical Engineer, M. Sc. Deparatmento de Ingenieria Ambiental. Universidad Libre Bogotá, andresf.lopez@unilibrebog.edu.co
FIDERMAN MACHUCA-MARTÍNEZ
Escuela de Ingeniería Química. Universidad del Valle, Cali (Colombia), fiderman.machuca@correounivalle.edu.co
Received for review August 26th, 2009, accepted March 4th, 2010, final version April, 18th, 2010
ABSTRACT: The compound parabolic collector (CPC) is a widely used technology in photochemical applications, like photocatalytic reactions. For kinetic purposes in this kind of reaction, the radiation distribution has to be well known, since the reaction rate is strongly dependent on the photon absorption rate. The present work develops a mathematical model which allows simulating the reflection of direct solar radiation on a CPC. Using analytical geometry and vector calculation, equations were evaluated, first for calculating the Cartesian coordinates of the reflecting surface. Later these points are used to calculate incident and reflected rays layouts on the collector. Visual Basic (Excel environment) program was developed for data generation and plotting the reflected rays at any instant. The incident radiation on the receptor was plotted separately displaying the daily direct energy distribution in the absorber. Also the involute length (collector) was calculated with these data, which can be very useful information for collector construction. Results obtained after simulations show that the distribution of incident energy on the absorber surface depends on the surface reflectivity. The incident energy is larger at the top of the absorber than the bottom zone and it is more convenient higher surface reflectivities for more uniform energy distributions. This mathematical model can be a first approach for absorption models which include direct solar radiation in photochemical or photothermal applications.
KEYWORDS: CPC, direct radiation, modeling, reflection.
RESUMEN: El colector parabólico compuesto (CPC) es una tecnología ampliamente usada en aplicaciones fotoquímicas, como las reacciones fotocatalíticas. Para propósitos cinéticos en esta clase de reacciones, se debe conocer la distribución de la radiación ya que la velocidad de reacción depende la absorción de fotones. En el presente trabajo desarrolló un modelo matemático que permitió simular el fenómeno de reflexión de la radiación solar directa en un CPC. Las ecuaciones se evaluaron usando geometría analítica y cálculo vectorial, primero para calcular las coordenadas cartesianas de la superficie reflectiva. Luego estos puntos se usaron para calcular las trayectorias de los rayos incidentes y reflejados en cualquier instante. La radiación incidente en el receptor se graficó independientemente, mostrando la distribución de la energía directa que llega directamente al absorbedor. La longitud de la involuta también se calculó a partir de estos datos, los cuales pueden resultar muy útiles para su construcción. Los resultados obtenidos a partir de las simulaciones muestran que la distribución de la energía incidente en la superficie del absorbedor depende de la reflectividad de la superficie del CPC. La energía incidente es mayor en la parte superior que en la inferior del absorbedor, y son más convenientes valores altos de reflectividad para distribuciones de energía más uniformes. Este modelo matemático puede ser una primera aproximación para modelos más complejos de absorción de fotones que incluyan radiación solar directa en aplicaciones fotoquímicas o fototérmicas.
PALABRASCLAVE: CPC, radiacióndirecta, reflexión
1. INTRODUCTION
The solar energy is an important part of the renewable energies. Their abundance and low cost are two great strategic advantages, that they turn it an excellent energy alternative for developed and developing countries. Since 1970, the research has been oriented to find ways to take advantage of the energy in a more efficient manner [1].
A low yield in the use of this kind of energy is one the major disadvantages respect to other conventional energy sources. In this aspect, the development of the solar concentrators becomes important, since they are devices that improve considerably the performance of systems which use solar energy for its operation. The most outstanding physical obstacle in these systems is the area that must be exposed for obtaining the maximum use of the solar energy, so the objective of a concentrator is to redirect the largest quantity of radiation to a certain available area. Most studies about collectors design [2-4] have been focused to improve the radiation-to-available area ratio. Different types of collectors have been proposed for obtaining the maximal amount of radiation redirected to a specific absorber.
The compound parabolic concentrators (CPC) are curved screens designed to redistribute the solar radiation such as diffuse and direct one, in cylindrical absorbers. The geometry of these collectors is determined by the form of the absorber, and it is very important to increase the use of the solar radiation [5]. Initially, this device was proposed to photothermal applications [2,6]. Nonetheless, the CPC has been mainly applied to the photochemical treatment of polluted water [7-12]. The solar detoxification of polluted wastewaters with CPC photocatalytic reactors has widely studied [5,7,8,12-15], with the modeling and scaling-up of these reactors as the most challenging aspects of the photochemical applications. The modeling of the radiation field is one of the most difficult tasks that has to be faced, and there are several works reported regarding to the solution of this problem. Arancibia-Bulnes et al. [16,17] developed an approach for modeling radiation fields in parabolic through collectors and CPC based in the so-called P1 model. Alfano et al. [18,19] have proposed a more rigorous approach that implies the numerical solution of the radiative transfer equation (RTE). Mueses et al. [20] made an approach based in an effective area of the absorber by fitting parameters to experimental data.
The modeling of direct solar radiation in a CPC can be made by using the "ray-tracing" technique. Although the first applications of this procedure was aimed to model shadows and 3-D solids [21-24], the reflection of radiation in a CPC has been also modeled by ray-tracing-based computer programs [11,25]. However, the obtained plots for reflected radiation in a CPC have been used only for descriptive purposes and they do not provide useful information for modeling or scaling-up this kind of photoreactors. In this work, the modeling work was aimed to generate the data that could describe the collector involute curve, which can be used in their later production by tools that use numeric control; and to obtain data and equations which can model how the incident rays in the adjacent regions to the absorber are reflected toward its body.
2. MATERIAL AND METHODS
A program was elaborated based on Visual Basic of Microsoft Excel XP, which generated a series of coordinates in the XY plane that describes the curve of the CPC, the circumference of the absorber, and the incident and reflected rays by the collector, starting from analytical geometry and vectors' calculus.
3. MATHEMATICAL EXPRESSIONS
The Cartesian plane origin corresponds to the circular absorber centre and (x,y) coordinates of the absorber circumference were calculated with the following equations:
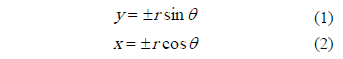
3.1. Compound Parabolic Concentrator
For the collector, the corresponding expression is an ordinary involute of the circumference before described, since the acceptance angle is equal to 90º (See figure 1). The general equations for acceptance angles [11] are given by:
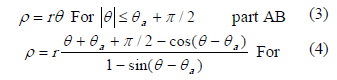
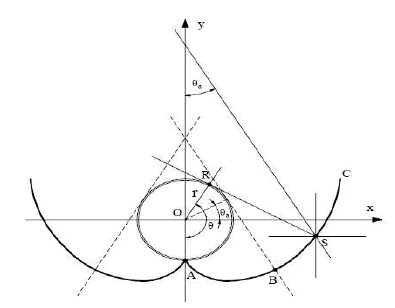
Figure 1. CPC acceptance angle
According to prior works [11], an optimum value for acceptance angle is between 60º and 90º. This value is used later for calculate the concentration ratio of the CPC according to the following equation:
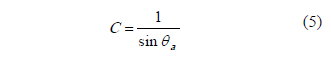
For constructing the CPC curve with Cartesian coordinates, expressions can be deduced starting from analytic geometry, where involute is built like a normal curve to the tangents that define the curve of the absorber [26], see figure 2.
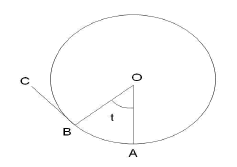
Figure 2. Involute construction
The BC segment corresponds to the OB radius perpendicular and its longitude corresponds to the AB circumference arch length and point C corresponds to an involute point. As point O is Cartesian plane origin, the coordinates of the point C are given by the following parametric equations:
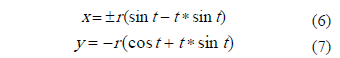
The t parameter corresponds to the angle AOB measured in radians from the OA axis and negative in counter clockwise.
3.2. Vectors expressions for reflection geometry
Considering a specular surface, then incidence and reflection angles respect to the perpendicular of reflecting surface are equal. Using parameterized equations (6) and (7), a vectorial equation for position r can be evaluated as follows:
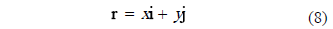
Where the unitary tangent vector T is given by the expression:
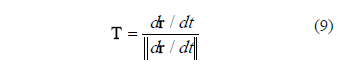
And the unitary normal vector N is given by this expression:
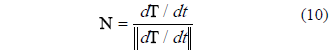
Where normal vector N is given by Eq. (10) after evaluating the corresponding derivatives, the following expressions were obtained:
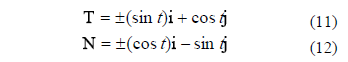
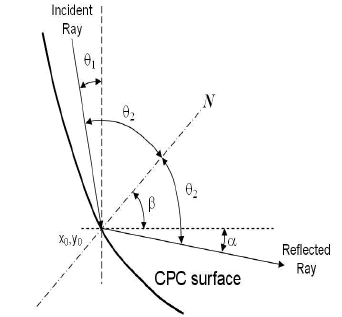
Figure 3. Incident ray trajectory on CPC surface
The N vector forms a b angle respect to the horizontal axis determined in the equations (9) and (10), and it can be calculated as follows:
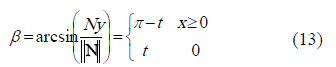
The incidence and reflection angles were estimated from the angle of the axis normal to the CPC surface (Figure 1) by considering the collector surfaces as specular. Eqs. (14-16) describe the reflection phenomenon as follows, (1)
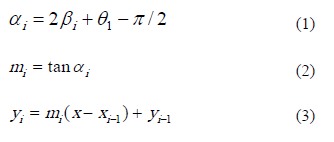
where i corresponds to a consecutive reflection on the CPC surface, q1 is the angle of the incident ray measured from the y-axis and a is the reflected ray measured from the positive x-axis. The reflected ray modeled by Eq. (16) can intercept a point on the reflective surface or the reactor wall. This was determined in an iterative process which estimated if the reflected ray hits the reactor wall before than the CPC surface. The reactor wall circumference is described by Eq. (17).

Eq. (16) was substituted in Eq. (17) resulting in a second grade equation that was solved with Eqs. (18-22):
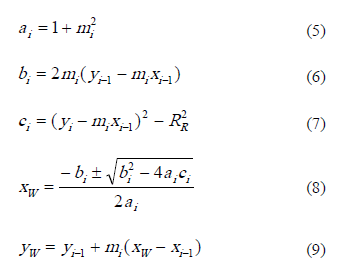
Eqs. (21-22) correspond to the coordinates of the points where the reflected ray could intercept the reactor wall. If these equations did not have real solutions, it means that the reflected ray intercepted a point on the CPC surface instead the reactor wall. In that case, the coordinates of this CPC point were estimated numerically due to the complexity of the analytical solution of the involved equations. The error-function developed in Eq. (25) allowed estimating the coordinates of such point.
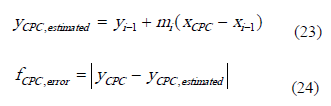
where xCPC and yCPC were calculated with Eqs. (6-7), and yCPC,estimated was calculated with the reflected ray equation (Eq. (23)). The error-function was evaluated for the points of the entire CPC involute, and the selected point was the one with the minimal error (fCPC,error).
After the necessary iterations, the coordinates where the ray was reflected by the CPC surface, as well where it hit the reactor wall, were calculated.
3.3. Reflectivity and incident energy on the absorber CPC
Incident energy (Einc) on the absorber surface given in (25) depends on the incoming energy (E0), surface reflectivity (r) and the number of successive reflections (n) on the specular surface of collector. This energy can be calculated from the Snell's law of reflectance as follows:
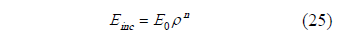
3.4. Sun path modeling
The sun movement in the sky was modeled from the elevation angle and the azimuth calculated values, from sunrise to sunset, for the corresponding latitude and longitude of the place where the collector will be located [27]. This model helped to obtain a complementary expression for calculating total incident energy of Eq. (25), where the solar time (t) can be calculated from incoming ray angle (q1) and declination (d):
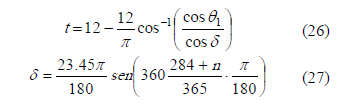
3.5. Calculation of CPC length
The integral of line was evaluated to determine the involute length in (28):
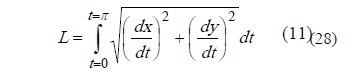
3.6. Algorithm flow sheet
The figure shows the algorithm flow sheet uses in the calculus
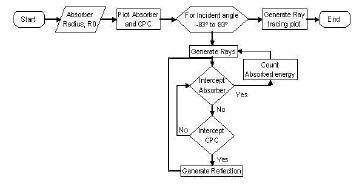
Figure 4. Algorithm Flow sheet
4. RESULTS AND DISCUSSION
Simulations were run varying incoming angle with 1º increments, generating 200 rays in each run (see figure 5). Each simulation provided an incident energy amount on the absorber surface. Although the incoming radiant energy value was taken arbitrarily, the distribution depended on the surface reflectivity. For photothermal or photochemical applications, reflectivity value can be adjusted to actual values of materials like ECP-244® and SA-85P® (both manufactured by 3M), present in commercial CPC used for water treatment [11].
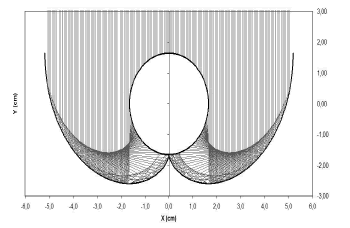
Figure 5. Ray-tracing with an incident angle of 0°
An acceptance angle of 90º was used for data generation of CPC involute plot. Involute covers until 7.9 cm approximately in horizontal axis, giving an additional area of irradiation to the absorber, as seen in figure 5. Even the absorber zones which were not exposed to direct radiation received some energy after successive reflections.
The picture of Figure 5 was comparable to the reported in literature [11,25] obtained from commercial computer programs. That points that the proposed equations were reliable and could model faithfully the reflection phenomenon of the solar direct radiation in a CPC. All the direct radiation that hit the collector surfaces could be reflected to the circular absorber as it was expected.
The total incident energy resulted from the summation of the incident energies of each run of simulation that corresponds to a specific incoming angle which varies depending on the sun position (azimuth and elevation angle).
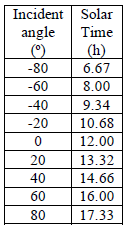
Table 1 shows data for a specific day (April 20th) considering that there is no surface azimuth angle, and the angle respect the horizontal surface is equal to the location latitude. For evaluating the direct incident radiation along this day, the solar time expression (26) based in declination value (which depends on the selected day of the year for the simulation) of equation (27).
Figures 6a, 6b and 6c show the energy distribution results of three different simulations varying the collector surface reflectivity. The circumference corresponds to absorber and the plot around it represents the energy distribution. When the energy distribution plot is located near the absorber surface means that this zone of the absorber received low amounts of incident energy, meanwhile if the plot is far from surface, the incident energy amounts are larger.
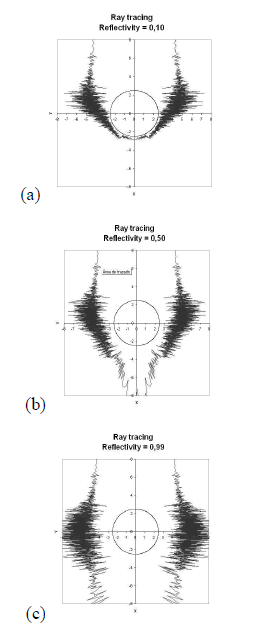
Figure 6. Incident energy on absorber surface for different reflectivities. a) 0.10, b) 0.50, c) 0.99
The incident energy plots provided a good idea of the behavior for the incident photon flux in photochemical applications. This information can be useful for studying the photon absorption effect in CPC solar reactors. This procedure can be coupled to mathematical models proposed in literature [11,16-18,28] for modeling the photon absorption phenomenon in photocatalytic reactions, and by this way, to estimate truly intrinsic rate laws for this kind of processes. The incident energy profiles were comparable to the obtained in a previous work carried out by Malato et al. [11]. This further observation confirmed that the model proposed in this study is valid for photochemical applications.
It was possible to calculate the involute length by using the Eq. (28). Numerical integration was used for this integral evaluation. For this case, with an absorber of 2.5 cm of radius, the length of the involute was equal to 12.34 cm. This data are very useful in collector construction since the sheet dimensions can be determined from them.
5. CONCLUSIONS
This model gives a good first approach for more complex mathematical models which involve total radiation including scattered and direct components. Also, it can be a useful tool for developing absorption models in photochemical applications, and obtaining more rigorous kinetic models in photocatalytic reactions which employ CPC as photoreactors.
The simulations with three reflectivity values showed that higher reflective materials give more uniform energy distribution, being more convenient for photochemical or photothermal applications which use solar radiation as energy source. Lower reflectivity values give poor incident energy distribution at rear zones of the absorber (as seen in Figure 6a).
By using simple expressions from analytical geometry and vectorial calculus, mathematical model can be obtained with reasonable rigor degree. This tool could model diffuse radiation with the help of a reliable random numbers generator.
ACKNOWLEDGEMENTS
Authors thank to the Vice-Head Office of Research of the Universidad del Valle (Grant 2520) and COLCIENCIAS by the financial support (Grant 110647922029).
REFERENCES
[1] ZEKAI S. "Solar energy in progress and future research trends". Prog. Energy Combust. Sci.,(30), 367-416, 2004. [ Links ]
[2] HATWAAMBO S., HAKANSSON H., NILSSON J., KARLSSON B. "Angular characterization of low concentrating PV-CPC using low-cost reflectors". Solar Energy Material and Solar Cells,92, (11), 1347-1351, 2008. [ Links ]
[3] Meinel A., Meinel M. Applied Solar Energy - An introduction. Reading - USA: Addison-Wesley Publishig Company; 1977. [ Links ]
[4] MOUSAZADEH H., KEYHANI A., JAVADI A., MOBLI H., ABRINIA K., SHARIFI A. "A review of principle and sun-tracking methods for maximizing solar systems output". Renewable and Sustainable Energy Reviews,13, (8), 1800-1818, 2009. [ Links ]
[5] S. Malato. "Photocatalytic reactors for the treatment of liquid wastewater in the presence of solar irradiation". Thessalonica. Vol. February, pp. 1-16. 2004. http://www.psa.es/webeng/projects/cadox/documents/Solarphotoreactors.pdf [ Links ]
[6] FASULO A., ODICINO L., PERELLO D. "Development of a CPC with low thermal losses". Solar & Wind Technology,4, (2), 157-162, 1987. [ Links ]
[7] AJONA J., VIDAL A. "The use of CPC collectors for detoxification of contaminated water: Design, construction and preliminary results". Sol. Energy,68, (1), 109-120, 2000. [ Links ]
[8] COLINA-MÁRQUEZ J., DÍAZ D., RENDÓN A., LÓPEZ-VÁSQUEZ A., MACHUCA-MARTÍNEZ F. "Photocatalytic Treatment of A Dye Polluted Industrial Effluent With A Solar Pilot-Scale CPC Reactor". J. Adv. Oxid. Technol.,12, (1), 93-99, 2009. [ Links ]
[9] MALATO S., BLANCO J., RICHTER C., CURCÓ D., GIMÉNEZ J. "Low-concentrating CPC collectors for photocatalytic water detoxification: Comparison with a medium concentrating solar collector". Water Sci. Technol.,35, (4), 157-164, 1997. [ Links ]
[10] MALATO S., BLANCO J., CÁCERES J., FERNÁNDEZ-ALBA A.R., AGÜERA A., RODRÍGUEZ A. "Photocatalytic treatment of water-soluble pesticides by photo-Fenton and TiO2 using solar energy". Catal. Today,76), 209-220, 2002. [ Links ]
[11] MALATO S., BLANCO J., MALDONADO R., FERNÁNDEZ P., ALARCÓN D., COLLARES-PEREIRA M., FARINHA J., CORREIA DE OLIVEIRA J. "Engineering of solar photocatalytic collectors". Sol. Energy,77, (5), 513-524, 2004. [ Links ]
[12] MALATO S., BLANCO J., VIDAL A., RICHTER C. "Photocatalytic decontamination and disinfection of water with solar collectors". Catal. Today,122, (1-2), 137-149, 2007. [ Links ]
[13] BAHNEMANN D. "Photocatalytic water treatment: solar energy applications". Sol. Energy,(77), 445-459, 2004. [ Links ]
[14] BANDALA E., ARANCIBIA-BULNES C., OROZCO S., ESTRADA C. "Solar photoreactors comparison based in oxalic acid photocatalytic degradation". Sol. Energy,(77), 503-512, 2004. [ Links ]
[15] MALATO S., BLANCO J., VIDAL A., RICHTER C. "Photocatalysis with solar energy at a pilot-plant scale: An overview". Appl. Catal. B-Environ.,(37), 1-15, 2002. [ Links ]
[16] ARANCIBIA-BULNES C., CUEVAS S.A. "Modeling of the radiation field in a parabolic trough solar photocatalytic reactor". Sol. Energy,(76), 615-622, 2003. [ Links ]
[17] ARANCIBIA-BULNES C., JIMÉNEZ A., ESTRADA C. "Development and Modeling of Solar Photocatalytic Reactors". Adv. Chem. Eng.,36), 185-227, 2009. [ Links ]
[18] ALFANO O., CASSANO A. "Photoreactor Modeling: Applications to Advanced Oxidation Processes". Int. J. Chem. Reactor Eng.,6, (P2), 1-20, 2008. [ Links ]
[19] ALFANO O., CASSANO A. "Scaling-Up of Photoreactors: Applications to Advanced Oxidation Processes". Adv. Chem. Eng.,36), 226-287, 2009. [ Links ]
[20] MUESES M., MACHUCA-MARTÍNEZ F., COLINA-MÁRQUEZ J. "Determination of Quantum Yield in a Heterogeneous Photocatalytic System Using a Fitting-Parameters Model". J. Adv. Oxid. Technol.,11, (1), 42-48, 2008. [ Links ]
[21] CHEN C., HOPKINS G. "Ray tracing through funnel concentrator optics". Appl. Opt.,17, (9), 1248-1259, 1978. [ Links ]
[22] KAJIYA J., VON HERZEN B. "Ray tracing volume densities". Comp. Graphics,18, (3), 165-174, 1984. [ Links ]
[23] RABL A. "Edge-ray method for analysis of radiation transfer among specular reflectors". Appl. Opt.,33, (7), 1248-1259, 1994. [ Links ]
[24] WARD G., RUBINSTEIN F., CLEAR R. "A ray tracing solution for diffuse interreflection". Comp. Graphics,22, (4), 85-92, 1988. [ Links ]
[25] GIMÉNEZ, J., CURCÓ, D. "Modelos Cinéticos y de radiación en sistemas fotocatalíticos" in: Eliminación de Contaminantes por Fotocatálisis Heterogénea. M. B., editor. CYTED, 2001. 189. www.cnea.gov.ar/xxi/ambiental/cyted/15cap09.pdf [ Links ]
[26] SARAVIA L. "Diseño gráfico de concentradores tipo CPC". Avances en energías renovables y medio ambiente,8, (1), 25-30, 2004. [ Links ]
[27] IDEAM. "Atlas Radiación Solar" in: Atlas de Radiación Solar de Colombia. Primera ed., Ministerio del Medio Ambiente, 2005. 133. [ Links ]
[28] LI PUMA G., TOEPFER B., PUDDU V. "Photocatalytic oxidation of herbicides in single-component and multicomponent systems: Reaction kinetics analysis". Appl. Catal. B-Environ.,(65), 1-10, 2006. [ Links ]