Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellín vol.9 no.17 Medellín July/Dec. 2010
A conceptual spatio-temporal multidimensional model
Un modelo multidimensional conceptual espacio-temporal
Francisco Moreno*; Jaime Alberto Echeverri Arias**; Bell Manrique Losada***
* Ingeniero de Sistemas, Ph. D(c). Profesor asistente Universidad Nacional Colombia. Correo electrónico: fjmoreno@unalmed.edu.co.
** M. Sc. Ing. de Sistemas, profesor Universidad de Medellín. Medellín, Colombia. Correo electrónico: jaecheverri@udem.edu.co .
*** M. Sc. Ing. de Sistemas, profesora Universidad de Medellín. Medellín, Colombia. Correo electrónico: bmanrique@udem.edu.co.
Abstract
Today, thanks to global positioning systems technologies and mobile devices equipped with tracking sensors, and a lot of data about moving objects can be collected, e.g., spatio-temporal data related to the movement followed by objects. On the other hand, data warehouses, usually modeled using a multidimensional view of data, are specialized databases to support the decision-making process. Unfortunately, conventional data warehouses are mainly oriented to manage alphanumeric data. In this article, we incorporate temporal elements to a conceptual spatial multidimensional model resulting in a spatio-temporal multidimensional model. We illustrate our proposal with a case study related to animal migration.
Palabras clave: data warehouses, multidimensional models, conceptual modeling, moving objects.Resumen
Hoy, gracias a los sistemas de posicionamiento global y dispositivos móviles equipados con sensores de rastreo, se puede recopilar una gran cantidad de datos sobre objetos móviles, es decir, datos espacio-temporales relacionados con el movimiento seguido por esos objetos. Por otro lado, las bodegas de datos, usualmente modeladas mediante una vista multidimensional de los datos, son bases de datos especializadas para soportar la toma de decisiones. Desafortunadamente, las bodegas de datos convencionales están principalmente orientadas al manejo de datos alfanuméricos. En este artículo, se incorporan elementos temporales a un modelo multidimensional conceptual espacial dando origen a un modelo multidimensional conceptual espacio-temporal. La propuesta se ilustra con un caso de estudio relacionado con la migración de animales
Key words: bodegas de datos, modelos multidimensionales, modelado conceptual, objetos móviles
INTRODUCTION
In the last decade Data Warehouses (DWs) [1, 2] have proved their usefulness as systems for integrating information and supporting the decision-making process. DWs are usually modeled using a multidimensional view of data [3]. A multidimensional model is a model of business activities in terms of dimensions and facts. A dimension is a categorizing structure by which factual data can be classified for analysis purposes. For example, in an animal resource consumption scenario, dimensions such as Time and Group of Animals can be used to analyze facts about animal consumption habits.
A dimension is organized in a hierarchy of levels [4] to enable the data analysis at various levels of detail, e.g., in the Time dimension, there exists a hierarchical relationship among days, months, and years, see figure 1. This hierarchical relationship captures the full containment between dimension values, e.g., a day is fully contained in a month, a month is fully contained in a year.
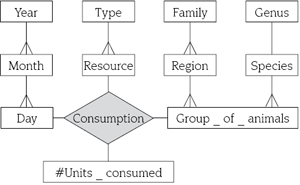
Figure 1. A conventional multidimensional model for analyzing animal consumption.
Source: authors
Conventional DWs are mainly oriented to manage alphanumeric data; however, in recent years DWs have been enriched with spatial data [5-10]. In particular, the work by Jensen [7] introduces the partial containment relationship between dimension values, a relationship prevalent in spatial data. For example, the location of a group of animals can be partially contained in a geographical region; some weeks are partially contained in a month. There are also proposals that provide support for managing temporal data in a DW, for a recent survey see [11]. Note that although DWs include a Time dimension, this dimension is not oriented to keep track of changes in other dimensions [10], e.g., when a group of animals changes its geographical region; therefore, additional temporal support is required for managing this sort of changes.
On the other hand, with the advance of technologies such as sensors and Global Positioning Systems (GPS), other types of data are becoming available in huge quantities, e.g., spatio-temporal data about migration of animals, movements of trucks, ships, airplanes, people, among others. We believe that the incorporation of this type of data into a DW can enable the discovery of spatio-temporal behaviors that otherwise would be very difficult to recognize.
There are a few works devoted to conceptual spatio-temporal multidimensional models. Savary [12] presents a UML class diagram for a spatio-temporal DW oriented to human motion in urban locations. What the authors call spatio-temporal is the combination of time intervals and locations, which are represented in an alphanumeric format. In Pestana [13] a conceptual spatio-temporal multidimensional model is proposed. Perceptory model [14] that provides a graphic notation for representing non-multidimensional spatio-temporal systems is used. The authors adopt spatial dimensions and spatial measures from the work by Han [5] and consider that their associated geometries can evolve over time. Ahmed [15, 16] proposes a conceptual multidimensional model for continuous spatial data, which deals with natural phenomena that exist continuously in time and space, i.e., that have unclear boundaries. However, none of these works consider partial containment or temporal relationships between dimension values.
In this paper, we gradually extend a conceptual spatial multidimensional model with temporal elements giving rise to a spatio-temporal multidimensional model where partial containment is supported and temporal relationships between dimension values are tracked.
The rest of the paper is organized as follows. In section 2 we develop our proposal and in section 3 we end the paper and present some remarks for future research.
1. FROM A CONVENTIONAL TO A SPATIO-TEMPORAL MULTIDIMENSIONAL MODEL
1.1 A conventional multidimensional model
Suppose we are interested in analyzing the resource consumption of groups of animals. The location of a group of animals is in a geographical region and we assume that all the animals in a group belong to the same species. Species are classified into genera and genera into families. Animals consume resources, e.g., grass, fruits, fish, insects, salt, water, which are categorized in types, e.g., vegetal, animal, mineral. Data about resource units (kg) consumed by each group of animals are recorded daily. A multidimensional model to represent this scenario is shown in figure 1. To represent our multidimensional models, we use basic notations from Malinowski [10], see figure 2, Note that, since the cardinality of every level (rectangles) participating in a fact relationship (grey diamond) is zero-to-many (crowfoot connector), such cardinalities are not showed in order to simplify the model.
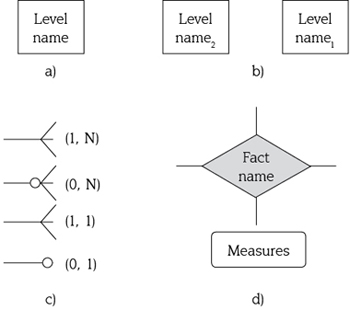
Figure 2. Basic notations for a conceptual multidimensional model: a) level,
b) hierarchy, c) cardinalities, and d) fact relationship.
Source: Malinowski [10].
Consumption fact relationship facilitates data analysis. For example, analysts can formulate queries such as what is the total number of units of water consumed in each geographical region? Which are the months when the water consumption increase (decrease)?
Note that if a visual representation of spatial data (for the regions and the locations of groups of animals) is added to our model, this would enable the discovery of patterns that otherwise would be difficult to recognize, as we show in the next section.
1.2 Incorporating Spatiality
In a multidimensional model, spatiality can be incorporated as an analysis axis, i.e., as a dimension, and/or as an analysis subject, i.e., as a fact [8]. We define a spatial dimension as a dimension that includes at least one spatial level. A spatial level is a level that the application needs to keep its spatial characteristics [10] represented by geometries. Spatial dimensions allow that facts be analyzed according to predefined spatial levels, as usual in a multidimensional model. On the other hand, facts can include spatial measures, i.e., measures represented by a geometry.
Geometries of spatial levels can be topologically related. Topological relationships for geometries have been identified [17-19], e.g., eight topological relation ships have been identified for regions: disjoint, meet, equal, inside, contains, coveredBy, covers, and overlap. Some of these relationships apply to other types of geometries, details are given in [18].
On the other hand, in conventional multidimensional models, the hierarchical relationship between levels captures their full containment [20], e.g., the location of a group of animals is fully contained in a geographical region. Full containment helps to ensure correct aggregation of measures in higher levels, e.g., the number of units consumed in a specific consumption fact is (indirectly) associated with a single geographical region. However, in practice full containment can be violated. We deal with this situation in subsection 2.3.
When spatial data come into play, the full containment relationship corresponds to the topological relationship inside/contains, coveredBy/covers, or equal, see figure 3.
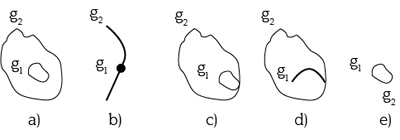
Figure 3. Examples of some topological relationships between geometries g1 and g2:
a) and b) inside/contains, c) and d) coveredBy/covers, and e) equal.
Source: authors
For representing the geometry of spatial levels and topological relationships, we use icons from Malinowski [10], see figure 4, that in turn, were based on the work by Parent [18]. We extend the multidimensional model of figure 1 in order to support topological relationships between levels, see figure 5.
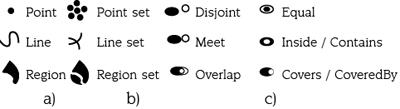
Figure 4. Notations for: a) simple geometries, b) complex geometries, and
c) topological relationships.
Source: Malinowski [10].
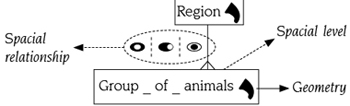
Figure 5. Spatial level, spatial relationship, and geometry of a spatial level.
Source: authors
Consider the topological relationship between Group_of_animals and Region levels. The location of a group of animals can be inside, covered by, or equal to a geographical region. We enrich Malinowski's conceptual model with the symbol ¦ (exclusive or) to express this topological constraint, see figure 5.
The addition of visual representation of spatial data enables spatial data analysis. For example, analysts can now formulate queries such as what is the total number of units of water consumed by all the groups of animals located within a given zone (a zone that can cover several geographical regions)? Is the resources' consumption higher in the east or in the west regions during the winter months?
1.3 Incorporating Partial Containment
In a multidimensional model summarizability is a property needed to ensure correct aggregation of measures. In order to guarantee summarizability, dimension hierarchies must meet disjointness and completeness conditions [21]. There is a third necessary condition for summarizability, but this depends on the correct use of measures with the aggregation functions applied [21]; therefore, it will not be discussed here. Informally, disjointness states that a member level can only be associated with a member level in each higher level, and completeness states that each member level must be associated with a member level in an immediate parent level, i.e., there do not exist “orphans” members.
In the model of figure 5, the location of a group of animals cannot be associated with more than one geographical region, otherwise disjointness condition would be violated. However, in real life the location of a group of animals could overlap several geographical regions. To represent this situation, we extend our model allowing the topological relationship overlap, see figure 6, between levels, i.e., the hierarchical relationship between levels captures their partial containment [7], see figure 7. In figure 8 we propose symbols in order to simplify our graphical notation to represent spatial full containment and spatial partial containment.
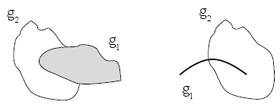
Figure 6. Examples of overlap relationship between geometries g1 and g2.
Source: authors
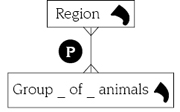
Figure 7. Allowing spatial partial containment
in our multidimensional model.
Source: authors
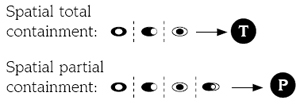
Figure 8. Symbols to represent spatial full
and partial containment.
Source: authors
Partial containment requires a special handling to ensure correct aggregation of measures because disjointness condition can be violated. For instance, suppose a group of animals overlaps regions r1 and r2, see figure 9, How should the number of units consumed by this group be aggregated with regard to regions r1 and r2?
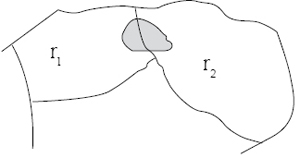
Figure 9. A group of animals located between two regions.
Source: authors
Note that, partial containment is a generalization of full containment and usually violates disjointness; however, it is possible, although hard, to think of an example where partial containment and disjointness must be met. For example, suppose that the location of a group of animals can be partially contained in just one region and regions are disjoint, see figure 10(a). Analogously, full containment usually meets disjointness; however, if regions are not disjoint, it is possible that full containment violates disjointness, see figure 10(b).
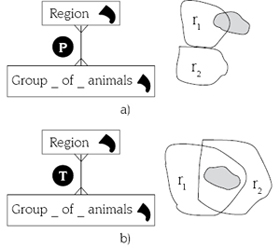
Figure 10. Containment and disjointness examples:
a) partial containment and disjointness and
b) full containment and non-disjointness.
Source: authors
So far, we have assumed that the location of a group of animals does not change during its lifespan. However, this assumption does not hold in scenarios such as animal migration, see subsection 2.4. Note that in our current model if the location of a group of animals changes, only the last location where the group is (or was) saved.
1.4 Incorporating Temporality
Consider a scenario of periodic animal migration [22], i.e., the movements of a group of animals among geographical regions, see figure 11. To represent this situation, we extend themodel of figure 7 with temporal elements. We consider time as discrete, i.e., a point in the time line that corresponds to a positive integer [23]. A positive integer represents an instance of a temporal unit, e.g., an hour, a day. Let i, j be positive integers, [i, j] represents an interval, i.e., a set of contiguous integers. For clarity, we will use d1 (or an equivalent value such as 2008-Jan-01) instead 1 to represent, e.g., day 1.
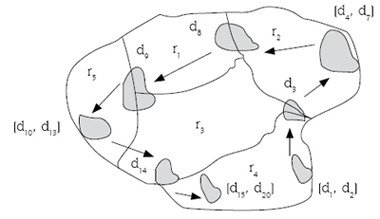
Figure 11. Migration among regions (ri) of a group of animals.
Source: authors
We add temporality to our model in two ways: i) we support temporal relationships, e.g., we keep track of the assignments between Group_of_animals and Region levels, and ii) we track the evolution of the geometry of a spatial level, i.e., a time-varying geometry.
In figure 12, the location of a group of animals can be associated with more than one geographical region at any time instant (day) and the corresponding partial containment relationship between these levels must also hold at any time instant.
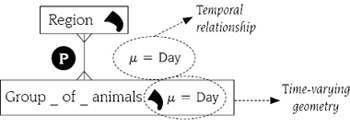
Figure 12. Temporal relationship and time-varying geometry.
Source: authors
With regard to the evolution of the geometry of a spatial level, the geometry can change of position, extent, or both at any time instant as long as the partial containment relationship between Group_of_animals and Region levels holds.
The addition of temporality to our model enables the analysts to formulate queries such as what is the total number of units of water consumed by a group of animals in its last two visits to a particular geographical region? What is the total number of units of water consumed by a group of animals in all its visits to a given zone?
2. CONCLUSIONS AND FUTURE WORK
We enriched a conceptual spatial multidimensional model with temporal elements giving rise to a spatio-temporal multidimensional model. We incorporated elements to represent spatio-temporal relationships between levels and to manage time-varying geometries of spatial levels. In addition, we proposed symbols to represent spatial full/partial containment between spatial levels.
As future work, we plan to transform our conceptual model into a logical one to facilitate their implementation in a particular paradigm. We also plan to develop a query language in order to express spatio-temporal multidimensional queries, such as the ones described through section 2. From a physical point of view, a related issue is how to store and retrieve efficiently these data. Data structures and indexing schemes must be designed for this purpose.
Analysis of summarizability when spatial partial containment arises is another promising direction for research, although there are some proposals [17, 24]; a definitive handling of this subject has not been achieved.
Finally, note that from figure 11, we can infer a trajectory from the evolving location of the group of animals. It could be interesting to model a trajectory explicitly, i.e., as a first class concept, in a multidimensional model. This could enable trajectory analysis, e.g., we could formulate queries such as how many trajectories cross a given region.
REFERENCES
[1] W. H. Inmon, Building the Data Warehouse, 4 ed., Hoboken: John Willey & Sons, Incorporated, 1993. [ Links ]
[2] R. Kimball et al., The Data Warehouse Lifecycle Toolkit, New York: Wiley Computer Publishing, 2008, p. 800. [ Links ]
[3] R. Agrawal et al., “Modeling Multidimensional Databases” presentado a 13th International Conference on Data Engineering (ICDE), 1995, pp. 10. [ Links ]
[4] R. Torlone, “Conceptual multidimensional models”, en Multidimensional databases, pp. 69-90: IGI Publishing, 2003. [ Links ]
[5] J. Han et al., “Selective materialization: An efficient method for spatial data cube construction”, en Research and Development in Knowledge Discovery and Data Mining, X. Wu, R. Kotagiri y K. Korb, eds., pp. 144-158, New York: Springer Berlin / Heidelberg, 1998. [ Links ]
[6] Y. Bédard et al., “Fundamentals of spatial data warehousing for geographic knowledge discovery”, en Geographic Data Mining and Knowledge Discovery, H. J. Miller y J. Han, eds., pp. 53-73: CRC Press, 2001. [ Links ]
[7] C. S. Jensen et al., “Multidimensional data modeling for location-based services”, The VLDB Journal, vol. 13, no. 1, pp. 1-21, 2004. [ Links ]
[8] S. Bimonte et al., “Towards a spatial multidimensional model”, presentado a Proceedings of the 8th ACM international workshop on Data warehousing and OLAP, Bremen, Germany, 2005, pp. 39-46. [ Links ]
[9] M. L. Damiani, y S. Spaccapietra, “Spatial Data Warehouse Modelling”, en Processing and Managing Complex Data for Decision Support, J. Darmont y O. Boussaïd, eds., p. 27, Lyon: Universidad de Lyon, 2006. [ Links ]
[10] E. Malinowski, y E. Zimnyi, Advanced Data Warehouse Design: From Conventional to Spatial and Temporal Applications New York: Springer Publishing Company, 2008. [ Links ]
[11] M. Golfarelli, y S. Rizzi, “A Survey on Temporal Data Warehousing”, International Journal of Data Warehousing and Mining, vol. 5, no. 1, pp. 17, 2009. [ Links ]
[12] L. Savary et al., “Spatio-Temporal Data Warehouse Design for Human Activity Pattern Analysis”, presentado a Proceedings of the Database and Expert Systems Applications, 15th International Workshop, 2004, pp. 814-818. [ Links ]
[13] G. Pestana, y M. Mira da Silva, “Multidimensional Modeling based on Spatial, Temporal and Spatio-Temporal Stereotypes”, presentado a ESRI International User Conference, 2005, p. 5. [ Links ]
[14] Y. Bédard et al., “Modeling Geospatial Databases with Plug-Ins for Visual Languages: A Pragmatic Approach and the Impacts of 16 Years of Research and Experimentations on Perceptory”, CoMoGIS 2004, vol. 3289, pp. 13-17, 2004. [ Links ]
[15] T. O. Ahmed, “Continuous Spatial DataWarehousing”, presentado a 19th International Arab Conference on Information Technology ACIT, 2008, p. 6. [ Links ]
[16] T. O. Ahmed, y M. Maryvonne, “Multidimensional Structures Dedicated to Continuous Spatiotemporal Phenomena”, presentado a 22nd British National Conference on Databases (BNCOD), 2005, p. 11. [ Links ]
[17] M. Egenhofer et al., “A Topological Data Model for Spatial Databases”, presentado a 1st Symposium of Design and Implementation of Large Spatial Databases, 1989, p. 15. [ Links ]
[18] C. Parent et al., “Spatio-temporal conceptual models: data structures + space + time”, presentado a Proceedings of the 7th ACM international symposium on Advances in geographic information systems, Kansas City, Missouri, United States, 1999, pp. 26-33. [ Links ]
[19] M. Schneider, “Computing the Topological Relationship of Complex Regions”, presentado a 15th Int. Conf. on Database and Expert Systems Applications, 2004, p. 9. [ Links ]
[20] T. B. Pedersen et al., “A foundation for capturing and querying complex multidimensional data”, Information Systems, vol. 26, no. 5, pp. 383-423, 2001. [ Links ]
[21] H.-J. Lenz, y A. Shoshani, “Summarizability in OLAP and Statistical Data Bases”, presentado a Proceedings of the Ninth International Conference on Scientific and Statistical Database Management, 1997, pp. 132-143. [ Links ]
[22] H. Dingle, y V. A. Drake, “What is Migration?”, BioScience, vol. 57, p. 8, 2007. [ Links ]
[23] A. O. Mendelzon, y A. A. Vaisman, “Temporal Queries in OLAP”, presentado a Proceedings of the 26th International Conference on Very Large Data Bases, 2000, pp. 242-253. [ Links ]
[24] I. Timko et al., “Probabilistic data modeling and querying for location-based data warehouses”, presentado a Proceedings of the 17th international conference on Scientific and statistical database management, Santa Barbara, CA, 2005, pp. 273-282. [ Links ]
Recibido: 23/08/2010.
Aceptado: 08/10/2010.