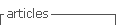Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Lecturas de Economía
Print version ISSN 0120-2596
Lect. Econ. no.71 Medellín July/Dec. 2009
ARTÍCULOS
The War on Drugs is Counterproductive, Once Again
La guerra contra las drogas es contraproductiva
La guerre contre la drogue est conteproductive
Carlos Humberto Ortiz*
* Carlos Humberto Ortiz: Universidad del Valle. E–mail: ortizc@univalle.edu.co. Postal Address: Universidad del Valle, Departamento de Economía, A.A. 25360, Cali, Colombia. I wish to express my gratitude to José Ignacio Uribe and Douglas Laing, who provided invaluable com– ments. As usual, the author is responsible for the whole text.
–Introduction. –I. Predictions from a Model on the Drug War. –II. A Modified Model. –III. Results under Different Assumptions on Productivity Change. –IV. The Government Budget Constraint. –V. The Relative Importance of Reducing the Demand for Drugs. –FinalComments. –References.
Abstract: A two–sector general equilibrium model that included drugs as basic goods was relatively successful at explaining the waste of resources that the war on drugs incurs (Ortiz, 2003). Due to the assumption of constant productivity, the model predicted the rise of the drug price with supply repression. Yet Plan Colombia, an unparalleled effort to eradicate drug production in Colombia, had no significant effect on drug prices. In order to correct the model two sources of productivity improvement in the drugs sector are examined. The modified model helps to understand why drug prices have remained stable, why global supply and demand have not diminished, and why coca plantations were spread throughout the nation under Plan Colombia.
Key words: Drug war, drug supply, drug demand, supply repression, basic good. Classification JEL: I12, K42, L11, O17, O41.
Resumen: Un modelo bisectorial de equilibrio general, que incluía las drogas como bienes básicos, fue relativamente exitoso para explicar el desperdicio de recursos que genera una guerra contra las drogas (Ortiz, 2003). Debido al supuesto de productividad constante, el modelo predijo que los precios de las drogas aumentarían con la represión y, sin embargo, el Plan Colombia no tuvo un efecto significativo en los precios. Para corregir el modelo, se examinan dos fuentes de mejoramiento de la productividad; con el fin de entender por qué los precios de las drogas se han mantenido estables y por qué la oferta y la demanda mundial no han disminuido, así como explicar las razones por las cuales los plantíos de coca se desperdigaron a lo largo y ancho del país bajo el Plan Colombia.
Palabras claves: Guerra contra las drogas, oferta de drogas, demanda de drogas, represión de la oferta, bien básico. Clasificación JEL: I12, K42, L11, O17, O41.
Résumé : Un modèle bisectoriel d'équilibre général qui considérait la drogue comme un bien de base a eu un relatif succès pour expliquer le gaspillage de ressources issues de la guerre contre les drogues (Ortiz, 2003). Ètant donnée l'hypothèse de productivité constante, le modèle prédisait que les prix des drogues augmenteraient avec la répression mais le Plan Colombie n'a pas eu un effet significatif sur la variation des prix. Pour corriger ce modèle, nous examinons deux sources d'amélioration de la productivité, ce qui permet de mieux comprendre les raisons pour lesquelles les prix des drogues ont été stables, et de savoir pourquoi l'offre et la demande mondiale n'a pas diminué, ainsi de savoir pourquoi les plantations de coca se sont repliées dans le pays avec la mise en œuvre du Plan Colombie.
Mots clé: Guerre contre la drogue, offre de drogues, demande de drogues, répression de l'offre, bien de base. Classification JEL : I12, K42, L11, O17, O41.
Introduction
The birth of Plan Colombia was greeted with moderate enthusiasm by El Tiempo, the highest circulation daily newspaper in Colombia. By that time the editor wrote that ''Plan Colombia is an unprecedented effort to confront drug trafficking that combines the repressive scheme [against production and consumption of drugs] with alternative development in coca–growing areas'' (El Tiempo, 2000, p. 1–26). This editorial pointed out that the repressive strategy had gone through several decades of failure; it recognized that after the investment of millions of million dollars, the drug market was unabated, violence had increased and institutional stability of the drug producing countries had been compromised. In spite of adverse past experiences, the editor expressed the hope that the new strategy –a mixture of stick and carrot– would prove that ''repression of drug supply has not failed due to a failure of the model, but because it has not been properly implemented'' (El Tiempo, ibid.). If the latter was the case, the editor added, the alliance of Colombia and the United States would fight and eventually win the war. But if it was not successful, our editor declared no more battles should be fought, and the United States would then have ''the historical responsibility to find and agree to the path of drug legalization, as it did many years ago, when it saw that alcohol prohibition was burning down the nation'' (El Tiempo, ibid.)
Nowadays, after ten years of augmented drug repression, and so much suffering, there are no longer any doubts as to the failure of Plan Colombia, at least from the point of view of declared objectives. Since 2000, Colombia and the United States have invested together more than one billion dollars per year (UNODC, 2006–2009), and yet the drug market continues to thrive unabated: prices do not rise, and consumption and production do not fall. Notwithstanding, the Colombian government is now asking for new taxes in order to launch, once again, the last battle. El Tiempo, for its part, seems to have forgotten its old editorial.
Given its academic rigour and international scope, it is convenient to quote a recent manifesto on the failure of the drug repression strategy. The Latin American Commission on Drugs and Democracy (LACDD, 2008) highlighted that Latin America is still the highest world exporter of marijuana and cocaine (and Colombia is the main exporter), production of opium and heroin shows a growing trend, drug consumption is growing in Latin America whilst it does not diminish either in the United States or Europe; eradication programs have mainly had local effects since crops are simply moved to different areas or countries without affecting the global market. Besides, the Commission stressed that the related drug business tentacles have penetrated the democratic institutions in the region, so that Latin Americans have witnessed ''the corruption of public servants, the judicial system, governments, the political system and, especially the police forces in charge of enforcing law and order'' (LACDD, 2008, p. 7). The Commission, under the leadership of ex–presidents Gaviria (Colombia), Cardoso (Brazil) and Zedillo (Mexico), has faced the facts and has dared to speak against the dominant political vision on drugs. Hence, this is a good time to reconsider the old repressive strategy. Since the drug problem is global, an international agreement is required to manage the problem. Nevertheless, this scenario is not an easy one, especially if it is understood that in the drug war all involved countries pay dearly but the United States reaps the lion's share of international drug profits. This paper is organized as follows. The introduction highlights the fact that the drug war has been largely ineffective. Predictions on the outcomes of the war on drugs from my model (Ortiz, 2003) are compared with the stark existing reality in the second section. Since the existing model did not consider the drug traffickers' productivity responses to augmented repression, a modified model is described and solved in the third section. Three contrasting drug productivity scenarios are examined in the fourth section. The drug war's tributary implications from the government budget constraint are analysed in the fifth section. A brief consideration on the advisability of reducing the demand for drugs is outlined in the sixth section. Some final comments close this paper in the seventh section.
I. Predictions from a Model on the Drug War
In order to understand why the war on drugs is counterproductive, I built a two–sector general equilibrium model where explicit consideration was given to drug trafficking activities (Ortiz, 2003). Under static and dynamic contexts, the model delivered some typical features of an economy specialized in drug activities and subject to drug supply repression:
i) The demand for drugs is price inelastic because of the addictive condition of consumption;
ii) The drug price is above marginal cost because the activity risk requires a premium;
iii) The drug sector delivers extraordinary profits;
iv) The drug price increases with drug repression;
v) The drug sector reproduces itself under supply repression;
vi) Openness of the economy leads to further specialization in illegal drug activities;
vii) Drugs repression diminishes the rate of economic growth both in the short–run and the long–run and
viii) In the long–run period, a higher degree of drug repression leads to higher taxes and a lower long–run growth rate.
All of these predictions, with the exception of the fourth (the rise of drug prices), have been confirmed by the experience of the drugs market:
i) Many analysts have estimated that demand for drugs is inelastic; using UNODC data for the Plan Colombia period, Mejía and Restrepo (2008) estimated the price elasticity of cocaine demand for drug dealers at the wholesale level in the U.S. as 0,67.
ii) According to different estimations, the cocaine price increases between 100 to 150 times from drug producing countries to the U.S. streets (Mejía and Restrepo, 2008; Reuter, 2008).
iii) Because the drug market delivers exorbitant returns, many illegal fortunes have been created both in producing and consuming countries.
iv) In real terms, drug prices decreased during the eighties, but since the nineties they remained relatively constant (LACDD, 2008; UNOCD yearly reports). This pattern was not affected by Plan Colombia!
v) Jails and cemeteries are full of drug traffickers, but they still keep coming. The situation is dramatic in the U.S.: whereas in 1980 fewer than 50.000 individuals were incarcerated by drug related crimes, by 2007 the number rose to 500.000 (LACDD, 2008). For Colombia and other drug producing countries, the history of the drug trade is a never ending succession of drug cartels and capos. The drug market is endowed with the Hydra property: it reproduces itself under attack (Ortiz, 2002, 2003).
vi) The comparative advantages of Colombia, based on the abundance of natural resources and also on social and political conditions that promote illegal activities, are strengthened as system of resource allocation as the economy opens its doors to the world markets: the trafficking of marijuana in Colombia started in the seventies with the substitution of the imports substitution model for the mixed model of protection and export promotion; the country diversified its activities to cocaine and heroin in the eighties with the reduction of non–tariff barriers and with further export promotion of protected industries and import promotion of raw materials, machinery and equipment; in the nineties, with the deepened orientation towards commercial and financial openness, drug traffic increased even more its operations scale (Ortiz, Uribe and Vivas, 2009).
vii) According to Cárdenas (2007), since 1980 the long–run rate of economic growth decreases in Colombia with the soaring violence unleashed by the expansion of drug trafficking activities.
viii) The Colombian National Ministry of Defence (NMD, 2009) reports that the growing expenditure on defence since the mid nineties was due mainly to the need to confront the military power of FARC – Colombian Revolutionary Armed Forces–, whose financial capacity had been increased significantly by drug trafficking. The same finance source, it has to be said, was used by other guerrilla movements and paramilitary organizations. Common criminal activities also went on the rise. As a result, the expenditure on defence as a fraction of GDP rose continuously from 2,2% in 1990 to 4,4% in 2000 (5,4% including U.S assistance), and it was subsequently increased even further to 5,3% in 2007 (5,6% including U.S. assistance). Moreover, government analysts envisage that expenditure in defence is going to remain above 5% of GDP (NMD, 2009). This is an incredibly high cost for a relatively poor country that has been fighting an endless war. Besides the cost of the war, public expenditure in Colombia also exhibits an increasing trend. Hence, tributary reforms to create contributions and increase tax rates are made on average every two years. Nowadays the government is preparing a new tributary reform aimed at financing public order, security and the drug fight.
In the light of the above continuing scenario, it is contended in this paper that my 2003 model was relatively successful at predicting the failure of the drug repression strategy. The model, however, predicted that the drug price would increase with supply repression. As seen above, the recent experience of Plan Colombia does not confirm this prediction. In spite of the strengthening of drug repression, drug prices have remained relatively unchanged, and the world supply and demand for drugs remained as high as ever. These features are extensively documented by the United Nations Office on Drugs and Crime – UNODC (1999 through 2009, 2009a).
The previous model's misspecification is found in the drug production function, since productivity was assumed to be constant. Using UNODC data, Mejía and Restrepo (2008) show that productivity in drug production increased significantly. Productivity per hectare in cocaine crops increased in Colombia from 4,25 to 7,86 kilograms per year between 1999 and 2006. In the same period, coca crops area fell from 162.000 to 82.000 hectares. Since area fell to half and productivity was almost doubled, total production remained relatively stable: final supply from Colombia fell from 561 tons to 474 tons. Although the Colombian supply of cocaine fell, final supply to consumer countries increased slightly from 718 to 745 tons. Hence, Peru and Bolivia compensated the effect of Plan Colombia. This is the so–called balloon effect: pressure somewhere is transmitted to the rest of the system. More recent data from the UNODC, as shown by figure 1, confirms the stability of the world supply of cocaine.
Therefore, higher productivity, both at the cultivation and drug processing level, higher efficiency at the distribution level –transportation methods and routes are now more sophisticated, including airplanes, submarines and go–fast boats that transport shipments by tons, and the balloon effect are responsible for the paradoxical result that drug repression has no effect on final consumer prices.
It has been pointed out that drug traffickers are not passive agents waiting for the government officials to eradicate their crops, to cut off their supply of arms and chemical inputs, to destroy their workshops, to seize their shipments, and to destroy their routes of trade. On the contrary, they behave as active agents when they aim at capturing the state in order to avoid the official action on them (Ortiz, 2007); they also behave as active agents, when they improve their productivity in order to compensate for the increased repression (Mejía and Restrepo, 2008); and they also behave actively, as it will be shown here, when they increase productivity by spreading drug production and trafficking throughout regions and countries of the Andean territory. Hence, the 2003 static model has been modified in order to analyze the productivity responses of the drug producing organisations to augmented supply repression. The issue of corruption is not addressed in this paper. International trade and economic growth are not examined either.
II. A Modified Model
This section is based on Ortiz (2003). The static model under autarky is modified by treating productivity of the drug technology as a variable. As added value, this paper includes a more careful consideration of the role of technological structure and technological change, the behaviour of drug firms under drug repression, a more detailed explanation of the long– run implications of the government budget constraint, and the role of drug addiction in the market demand. The paper also includes a graphical scheme to make comparative static analysis in the general equilibrium setting.
A. Household Behaviour
People consume two types of goods. One of them is a basic good. A suitable representation of these preferences is given by the Stone–Geary utility function: U(yd, qd) = θlog yd + log(qd – α), where qd is the quantity consumed of the basic good, α denotes the minimum consumption level of this good –the addiction measure, yd is the quantity consumed of the y–good, and θ is an index of consumption bias towards the y–good. Each consumer maximizes this utility function subject to the budget constraint: yd +pqd = I, where I is the consumer's income, and p is the relative price of the basic good. This operation yields the consumer demand functions:
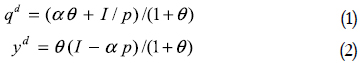
These expressions will be used later to determine the contribution of different agents to aggregate demand. Note that price elasticity of the basic good is always lower than 1: –(∂qd/∂p)(p/qd)=I/(I+θαp)<1
B. Technologies
The y–good is produced with a linear technology in labour: y = A(1 – n) L, where A is the constant productivity index of this sector, L is the available labour force, and (1–n) is the labour fraction hired by the sector producing good y.
The basic good technology is characterized by a decreasing marginal productivity of labour; i.e. qi=Φ(·)q(ni), q(0) = 0, q' > 0, q'' < 0, where qi is the drug production of the i–th firm, ni is the i–th firm's labour demand, q(ni) is a concave function in ni, and φ(·) is the productivity level which might depend on several factors. The explicit consideration of drug productivity as a variable is the single model innovation; it seems to be innocuous, but it will do the job.
There exists a rationale for the technological structure of the drug firm. The drug sector is characterized by strong entry barriers. Costs of entrance are high because the firm's activity implies a strict control over important fixed factors (land, workshops, entry and exit routes, entrepreneurial ability and knowledge, qualified staff and, fundamentally, contacts). So, it is assumed that there are just m firms in the period of analysis. Vertical integration is also assumed; i.e. each firm controls its own inputs, crops, drug production and trafficking. Integration is not only a simplifying assumption, it is also realistic since the whole operation under prosecution and criminalization requires a comprehensive control. Labour delivers a decreasing marginal product at the firm's level because fixed factors prevent the short–run replication of firms. Under these conditions the model yields extraordinary profits in the basic good activity.
C. Behaviour of Firms
Profits in the y–good sector are defined as after–tax income less labour costs: ΠY = (1 – τ)A(1 – n)L – w(1 – n)L where τ is the income tax and w is the wage rate. Given that profits are linear in labour and the market environment is competitive, profits in this sector must be nil. Hence, wages are equalized to labour productivity after taxes:
w = (1 – t)A (3)
The basic good activity is subject to repression. Firms in this activity face a probability of interdiction and destruction of the product equal to z. Hence, the firm's objective in the basic sector is to maximize expected profits, which are given by the following expression: E[Π(ni)] = (1 – z)[ pφ(·) q(ni) – wni] + z(–wni) where ni is the demand of labour by the i–th firm in this activity. Firms in this sector do not pay taxes since they are illegal.
The first order condition for maximization implies the equalization of the wage rate to the expected value of marginal product of labour:
w = (1 – z)p φ(·) q'(ni) (4)
Substitution of this equation into the expected profit expression of the basic good sector yields a more compact expression:
E[Π(ni)] = (1 – z) pφ(·)[ q(ni) – niq'(ni)] > 0 (5)
Expected profits in this sector are positive because of the concavity of the production function [average product is higher than marginal product: φ(·)q(ni) /ni > φ(·)q'(ni).
D. Relative Price
Equating equations (3) and (4) solves for the relative price of the basic good:
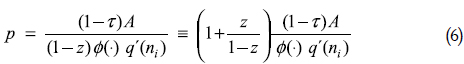
The expression z/(1–z) is the risk–premium of the basic–good activity. It increases very rapidly with z; in fact, as z converges to 1 –its maximum value, the risk–premium goes to infinity.
E. Labour Market Equilibrium
Assuming that labour supply is absolutely inelastic and that there are m identical firms in the basic–good sector, equilibrium in the labour market implies (1–n)L + mni = L, thus labour demand in the basic–good firm is given by
ni = nL / m (7)
A brief consideration is in order. In strict sense, the size of a basic good firm depends on the amount of fixed factor it controls (i.e., more land implies higher labour demand). In order to simplify the analysis and arrive to a symmetric solution, it is assumed from now on that all firms have access to the same amount of fixed factors.
F. Goods Supply
Taking into account the labour allocation to the basic good firm [equation (7)], the aggregate expected supply of the basic good is given by the following expression:
m E (qs) = (1 – z)m Φ (·) q (nL / m) (8)
The potential production of the basic good is given by mφ(·)q(nL/m), but government repression implies the destruction of a fraction z of this product. The supply of the y–good is given by: ys = (1–t)A(1–n)L. This sector is not subject to repression, but a fraction τ of the product goes to the government as income taxes.
G. Demand for the Basic Good
There are three markets in this economy: the labour market, the basic good market and the y–good market. According to Walras' law, one only needs to characterize the equilibrium in two markets in order to find the aggregate equilibrium. Thus, given that the equilibrium in the labour market was already defined, the equilibrium in the basic good market is characterized now.
Since preferences are non homothetic, the consumption mix changes with the level of income. Thus, aggregate demand has to be carefully specified; it ought to take into account the society income distribution.
In the period of analysis each worker earns the wage rate, w = (1–τ) A [equation (3)]; thus, according to equation (1), his demand for the basic good is given by
qwd = [α θ + (1 – τ) A/p ] / (1 + θ) (9)
Profits of the i–th firm in the basic good sector are given by equations (5) and (7). Thus, the demand for the basic good of the entrepreneur in this sector is given by
qid = { [α θ + (1 – z)φ(·) [ q(nL / m) – (nL/m) q'(nL/m)]} / (1 + θ) (10)
Aggegate demand for the basic good is given by
Qd = qwd L + qid m(11)
H. General Equilibrium
The equilibrium of the basic good market is found by equating expected supply and demand: mE(qs) = Q d, where the respective expressions are equations (8) and (11). In order to solve, one has to take into account the demand from the different agents [equations (9) and (10)], the equilibrium relative price [equation (6)], and the labour equilibrium condition [equation (7)]. After some algebra one obtains:
θ q(nL/m) – (1 – n)(L/m)q'(nL/m) = α θ (1 + L/m) / [(1 – z)φ(·)] (12)
This equation defines n, the labour allocation to the basic good sector. If the basic–good sector's productivity is high enough, the solution for n exists, it is unique and interior. Proof: The left–hand side expression of equation (12), represented by the thick line in figure 2, is increasing in n; it goes from a negative value, –(L/m)q'(0), for n = 0, to a positive value, θq(L/m), for n = 1. Given that the right–hand side expression of equation (12) is positive, it is represented by the dotted line of figure 2, the solution for n (= n*) is necessarily positive. For this solution to be lower than 1, the left–hand side expression of equation (12) for n = 1, must be higher than the right–hand side expression: θ q(L/m) > αθ (1 + L/m) / [(1–z)φ(·)] which implies (1–z)mφ(·)q(L/m) > α (m+L): the expected supply of the basic good when all labour resources are allocated to this activity should be enough to satisfy the basic–good minimum consumption requirements of L workers and m entrepreneurs of the basic–good sector.
I. Profits and Labour Demand in the Basic–Good Sector
It was already established that this model yields positive profits in the basic–good sector. It is convenient to check the direct relationship between profits and labour demand of this sector in the general equilibrium. Substitution of equations (6) and (7) into equation (5) yields another expression for the expected profits of the typical firm of the basic good sector: 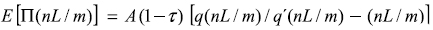 .
.
Partially differentiating with respect to the labour demand of the firm, nL/m, one obtains the mentioned positive relationship 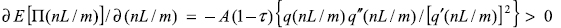 .
.
This result is not surprising since firms producing the basic good maximize expected profits and the choice variable is labour demand.
III. Results under Different Assumptions onProductivity Change
A. Constant Productivity
This is the case which is analyzed in the 2003 paper. The productivity level in the drug sector is assumed to be a constant: φ(·) = φ. Implicitly differentiating n with respect to z in equation (12) yields the following result:
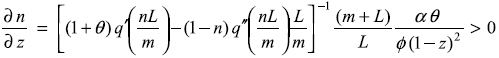
Since the right–hand–side expression is positive, the labour allocation to the basic good sector, n, increases with government repression to this activity, z. Note that for this result to follow it is required that the sector produces a basic good (α > 0). In graphical terms, this result is depicted by an upwards movement of the dotted line in figure 2, so that labour allocation to the basic sector, n*, increases.
Another result from the model under the assumption of constant productivity is that repression of the basic good sector increases the relative price of this good. In order to see this we substitute equation (7) into equation (6) and differentiate with respect to z:
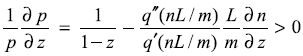
Hence, drug repression is counterproductive because supply contraction under inelastic demand increases the price and the sector's income, leading to higher expected profits and higher labour demand.
B. Higher Productivity by Technological Change
The experience of Plan Colombia has shown that drug producers found some ingenious ways of preventing coca–crops damage from aerial spraying of herbicides –tree pruning techniques, chemical screens, etc. They also managed to increase crops productivity –improved seeds, improved planting techniques, etc. Besides, drug traffickers are using now more efficient ways to transportation of chemical precursors, inputs, arms and drugs (submarines and submersible artefacts are frequently captured along the coasts of Colombia). Thus, the drug activity as a whole process has been able to defend itself by increasing efficiency. Let us then assume that the drug production function at the firm level assumes the following form: 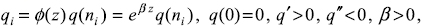 where productivity, φ(z) = e β z, increases with the drug repression index, z. By keeping everything else equal, the general equilibrium is defined by equation (12) with a minor modification: the denominator of the right– hand–side expression adopts the following form: (1–z) e β z. By differentiating the log of this expression with respect to z, one finds the derivative to be given by β–(1–z)–1. Hence, if β = (1–z)–1, productivity increases as much as necessary to compensate the augmented drug repression. In this case, labour allocation does not change (the dotted line in figure 2 does not change), ∂n/∂z = 0, and, as we will see now, the drug price and expected aggregate supply are unchanged as well.
where productivity, φ(z) = e β z, increases with the drug repression index, z. By keeping everything else equal, the general equilibrium is defined by equation (12) with a minor modification: the denominator of the right– hand–side expression adopts the following form: (1–z) e β z. By differentiating the log of this expression with respect to z, one finds the derivative to be given by β–(1–z)–1. Hence, if β = (1–z)–1, productivity increases as much as necessary to compensate the augmented drug repression. In this case, labour allocation does not change (the dotted line in figure 2 does not change), ∂n/∂z = 0, and, as we will see now, the drug price and expected aggregate supply are unchanged as well.
According to equations (6) and (7), and the productivity equation, φ(z)=eβ z, the price equation adopts the following form: 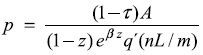
It can be seen immediately that the expression (1–z) eβz and the labour allocation to the sector, n, will not change with the drug repression index, z, if the productivity parameter β is equal to (1–z)–1. Hence, the drug price will not change either (∂p/∂z = 0).
Now, total expected supply of drugs is given by equation (8): mE(qs) = m(1 – z)eβz q(nL / m), where use is made of the productivity equation, φ (z) = eβz. In this case, it is also true that if the productivity parameter β is equal to (1–z)–1, the expression (1–z) eβz and the labour allocation to the sector, n, do not change with the drug repression index, z. Hence, total expected supply does not change either.
In summary, a proper technological change response to drug repression may compensate the damage from drug repression and leave the market unchanged.
C. Higher Productivity by Spreading the Activity
As explained earlier, the drug producing sector depends on several kinds of fixed factors. Let us assume now that a mixed index of all these factors is given by F, and that the firm's technology is of the Cobb–Douglas form: qi = φ(·)q(ni) = (F/m)µ (nL/m)1 – µ, where μ is the output elasticity of the fixed factor (a constant fraction), and 1–μ is the output elasticity of labour. It is assumed the each firm controls the same fraction of the fixed factor, F/m, and hires the same number of workers, ni = nL/m. The firm's technology is characterized by constant returns to scale in the fixed factor and labour. However, by definition, each firm is unable to expand this factor in the short–run period. Under this condition, labour experiences a decreasing marginal productivity. However, if drug repression leads the firms to acquire more of the fixed factor, the effect on labour productivity is equivalent to an improvement of technology. Hence, the productivity equation, φ(F/m), is assimilated to (F/m)μ; and the function q(nL/m) is defined as (nL/m)1–μ.
By keeping everything else equal, the general equilibrium is defined by equation (12) with a minor change, the denominator of the right–hand– side expression adopts the following form: (1–z)(F/m)μ. By differentiating the log of this expression with respect to z, and setting it to nil, one finds that this expression will not change if (1/F )(∂F/∂z) = [μ (1–z)]–1 > 0. As usual, the number of firms, m, is considered constant. Thus, if under drug repression, the firms seek to expand their fixed factor, as the above equation shows, labour allocation does not change, and, as it will be shown now, the drug price and the aggregate expected supply do not change either.
According to equations (6) and (7), the price equation adopts the following form:
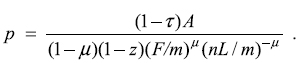
It can be seen immediately that the expression (1–z) (F/m)μ and the labour allocation to the sector, n, will not change with the drug repression index, z, if the fixed factor expands at the rate shown above. Hence, the relative price will not change either.
Total expected supply is given by equation (8): 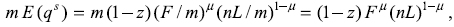 where use is made of the production equation. In this case, it is also true that by expanding the fixed factor at the rate shown above, the expression (1–z)Fμ and the labour allocation to the sector, n, do not change with the drug repression index, z. Hence, total expected supply does not change either.
where use is made of the production equation. In this case, it is also true that by expanding the fixed factor at the rate shown above, the expression (1–z)Fμ and the labour allocation to the sector, n, do not change with the drug repression index, z. Hence, total expected supply does not change either.
Some further evidence that this effect works is provided by the quick spreading of coca plantations across the Colombian states as Plan Colombia increased drug supply repression. As table 1 shows, in 1999, before Plan Colombia, only 12 out of 32 Colombian states were coca growers, and the activity was highly concentrated (only two states, Putumayo and Guaviare, had 54,2% of plantations); with Plan Colombia the activity was very swiftly spread, so that by 2008 the cultivated area is distributed among 24 states and the concentration is much lower.
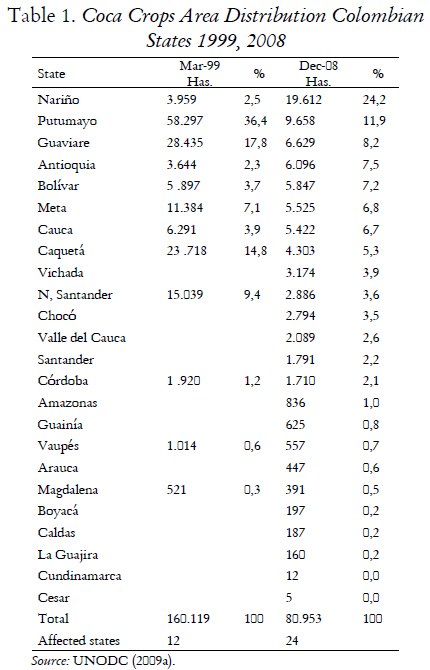
Even though drug firms are using now less hectares per crop, they move across a much higher territory. It is this movement which implies accumulating fixed factors and increasing labour productivity at the drug firm level.
This statement requires some explanation. For it to make sense it is necessary to differentiate between drug firm and coca crop; actually, each firm might control several crops as a result of vertical integration. Controlled land for illegal crops is of course a fixed factor at the level of the drug producing firm. However, land is not the highest binding constraint of the drug business. By making a small investment that implies intermingling illegal with legal crops, or by colonizing (and deforesting) the huge abandoned rural areas of Colombia, land is easily acquired for drug production. The costs associated to this process are small in private terms but huge in social terms: they are assumed primarily by the environment through further degradation. Thus, it is perhaps much more important as fixed factors the entrepreneurial ability and the net of contacts required to manage access routes (for seeds, precursors, other inputs, arms, etc.), transport means and routes for drugs, financial movements and money laundering, official corruption, reliable staff, security of the whole process, etc.
In summary, a proper expansion of the firm's fixed factors, expressed in an expansion of the area under control, a wider net of contacts for drug production and trafficking, and a higher number of trustworthy operatives for controlling the expanded activity, may compensate the damage of higher drug repression and leave the drug market unchanged. Therefore, the dispersion of drugs activity throughout the national territory strengthens the drug sector.
Three brief considerations are in order. First, the dispersion process is not only restricted to the Colombian territory; as mentioned before, Plan Colombia induced a partial transference of the activity to Peru and Bolivia, keeping global production levels stable. Second, if land were the single fixed factor of the drug sector, profits could be considered as land rents; given the relatively high supply of land in Colombia for coca production, there would be no explanation for the extraordinary profits of the drug sector. Hence, some other fixed factors must be involved in drug production. Third, there may be some difficulties understanding this analysis because the net of contacts is not an asset as tangible as land or physical capital. But the net of contacts is, indeed, an asset for drug firms as they could not operate without it. Moreover, as any other stock, the net of contacts ought to be accumulated and is subject to depreciation (contacts ought to be replaced when they are lost).
IV. The Government Budget Constraint
So far it has been assumed that the tax rate, τ, and the probability of interdiction and destruction of drugs, z, are policy variables. So they are assumed as constants. This may be true in the short–run period, or even in the long run whilst the government can afford to run deficits. In the very long–run period, however, someone has to pay for governmental programs as Plan Colombia. An interested foreign government may help, but it pays only a fraction, and for a limited period. Hence, in the spirit of Barro's 1990 paper, it is assumed here that in the very long–run period the government runs a balanced budget. It is assumed as well, in favour of discussion, that the government is efficient and no government funds are diverted to some other purposes. Without loss of generality, let us assume that the cost of destroying a unit of drugs (through eradication or shipment seizures) is a unit of the y–good. In this context, the government budget constraint (GBC) adopts the following form: τy = zmq. The left–hand side expression is the tax revenue that the government collects from the legal sector of the economy; the right–hand side expression is the cost of the expected number of destroyed drugs. Hence, the tax rate, τ, becomes a policy determined variable. Using the production functions, the GBC is rewritten as follows: τA(1–n)L = zmφ(·)q(nL/m), where the y–sector productivity (A), labour supply (L), and the number of drug producing firms (m) are assumed as constants. The drug sector productivity, φ(·), might be a constant or a function of z, as explained before. By taking logs and differentiating with respect to z, one obtains: 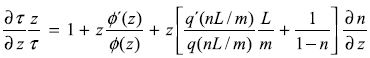
The three cases considered in the previous section are captured in this equation. First case, if the drug sector productivity is constant, φ'(z) = 0, the labour allocation to the drug sector increases with drug supply repression, ∂n/∂z > 0. In the second and third cases, it is considered that drug repression leads to a productivity increase in the sector, φ'(z) > 0, so that labour allocation does not change, ∂n/∂z = 0. Intermediate situations are also plausible. In any case, the long–run tax elasticity with respect to the probability z is higher than 1. Hence, an increased drug repression program will imply, sooner or later, higher taxes.
Without taking into account the negative growth implications of higher taxes, which are out of consideration within the context of this static model (see Ortiz, 2003), this model does yield that drug repression is welfare diminishing because it takes resources from the economy in order to throw them into the drug war. Moreover, as politicians in charge are subject to huge internal and external pressures to exhibit more effective results in the drug war, the government has to increase taxes in a more than proportional way.
V. The Relative Importance of Reducing theDemand for Drugs
It is worth noting that a change of tastes that takes consumers away from drugs hurts the drug sector. By implicitly differentiating equation (12) with respect to θ, the bias towards the y good, one obtains:
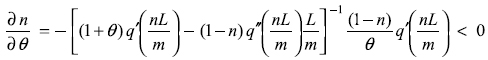
Since this derivative is unambiguously negative, it implies that a change of tastes towards the y–good diminishes the drug sector labour demand, diminishes aggregate demand for drugs, and shrinks drugs profitability.
A similar result is obtained if the degree of addiction lowers. As equation (12) and figure 2 show, a reduction of the addiction index, α, moves the dotted line downwards and implies an unambiguous reduction of the labour demand from the drugs sector:
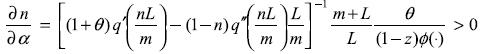
The problem with these results is that preferences (and their parameters, α and θ) are not discrete variables. And even if they could change (through education campaigns, health support to drug addicts and, perhaps, social integration processes), they only impinge on the demand side of the market. Hence, according to the above results, education and health support may be good measures for ameliorating the problems of drugs consumption, but they do not solve the problems caused by the repression of drug supply.
Final Comments
Given the negative externalities of drug consumption, and the problems derived from drug repression, there is a growing agreement on the necessity of resorting to some form of regulation of the drugs market. Becker, Murphy and Grossman (2006) have proposed controlled legalization with high consumption taxes, as it was done with alcohol. This important regulation issue is not, however, the objective of this paper.
My model (Ortiz, 2003) was built to explain the waste of resources and the welfare losses that the drug war brings. I contend that this model, even though it is small and simple, captures the relevant structural elements of the economy under repression of drugs supply. Actually, it was relatively accurate at predicting the economic consequences of the drug war that are mentioned in the introduction. All facts were, however, not exactly replicated because the model predicted the rise of the drug price as drug repression increases. In spite of increased drug repression, especially since the implementation of Plan Colombia, the real price of drugs has been relatively stable, and so it follows with the world market for drugs. A key element to understand this behaviour is the quick productivity responses of drug producers and drug traffickers to supply repression.
Hence, in order to fit the facts, this paper corrects the original model's inaccuracy by explicitly modelling the productivity of the drug sector. Two non–excludable sources of productivity improvement are analyzed: i) technological change and, ii) dispersion across the Andean territory with accumulation of the fixed factors required for drug production. The model shows that under supply repression some minimum levels of productivity improvements in the drug sector leave unaffected the relative drug price and the drug market.
Hence, the new model also embodies the Hydra property of the drug sector: under attack, drug firms become more productive, and the final global demand for drugs is served as always, just as predicted by Friedman (1972, 1991) and Barro (2000). Consistent neoliberal analysts do recognize the power of market forces.
In hindsight, the new model is more accurate and confirms the prediction that the drug war is not only self–defeating but counterproductive. This conclusion is reached even without taking into account all the negative externalities derived from the drug war and drug consumption (violence, health deterioration, incentive distortions, worsening income distribution, corruption, fiscal crisis, diminished economic growth, and growing environmental damage).
References
1. BARRO, Robert (1990). ''Government Spending in a Simple Model of Endogenous Growth'', Journal of Political Economy, Vol. 98, No. 5, pp. S103–117. [ Links ]
2. BARRO, Robert (2000). ''To Beat Colombia's Guerrillas, Legalize Drugs in the U.S.'', Business Week, March 13, p. 26. [ Links ]
3. BECKER, Gary; Kevin, MURPHY and Michael, GROSSMAN (2006). ''The Market for Illegal Goods: the Case of Drugs'', Journal of Political Economy, Vol. 114, No. 1, pp. 38–60. [ Links ]
4. CáRDENAS, Mauricio (2007). ''Economic Growth in Colombia: a Reversal of 'Fortune'?'' Ensayos sobre Política Económica, Vol. 25, No. 53, pp. 220–258, Banco de la República, Bogotá. [ Links ]
5. EL TIEMPO (2000). ''The Last Battle'', 8 de octubre de 2000, p. 1–26, Free translation [ Links ]
6. FRIEDMAN, Milton (1972). ''Prohibition and Drugs'', Newsweek, mayo 1, p. 104. [ Links ]
7. FRIEDMAN, Milton (1991). ''The War We Are Losing'', Searching for Alternatives: Drug–Control Policy in the United States, Melvyn P. Krauss y Edward P. Lazear, eds. Stanford: Hoover Institution Press, pp. 53–67. [ Links ]
8. LACDD – LATIN AMERICAN COMMISSION ON DRUGS AND DEMOCRACY (2008). Drugs & Democracy: Towards a Paradigm Shift, Disponible en: http://www.drogasedemocracia.org/Arquivos/livro_ingles_02.pdf (21 de julio de 2009) [ Links ]
9. MEJíA, Daniel and RESTREPO, Pascual (2008). ''The War on Illegal Drugs Production and Trafficking: An Economic Evaluation of Plan Colombia'', Documentos CEDE, No. 19, Universidad de los Andes, Bogotá, October. [ Links ]
10. NATIONAL MINISTRY OF DEFENSE – NMD (2009). Gasto en Defensa y Seguridad 1998–2011, Estudio No. 02, Dirección de Estudios Sectoriales, January. [ Links ]
11. ORTIZ, Carlos Humberto (2002). ''Luchando Infructuosamente contra la Hidra: un modelo sencillo del narcotráfico'', Cuadernos de Economía, Vol. XXI, No. 37, Universidad Nacional, Bogotá. [ Links ]
12. ORTIZ, Carlos Humberto (2003). ''La Guerra Contra las Drogas es Contraproducente: un análisis económico de Equilibrio General'', Lecturas de Economía, No. 58, pp. 47–68, Universidad de Antioquia, Medellín. An English version, ''The Drug War is Counterproductive: A General Equilibrium Analysis'', was presented in the 8th Congress of the Latin American and Caribbean Economic Association – LACEA, Puebla (Mexico), October. [ Links ]
13. ORTIZ, Carlos Humberto (2007). ''La Crisis Perpetua'', El Observador Regional, No. 1, Centro de Investigaciones y Documentación Socio– Económica (CIDSE), Universidad del Valle, Cali. [ Links ]
14. ORTIZ, Carlos; URIBE, José Ignacio, y VIVAS, Harvy (2009). ''Transformación Industrial, Autonomía Tecnológica y Crecimiento Económico: Colombia 1925–2005'', Archivos de Economía, No. 352, Departamento Nacional de Planeación (www.dnp.gov.co), Bogotá. [ Links ]
15. REUTER, Peter (2008). ''Assessing U.S. Drug Policy and Providing a Base for Future Decisions'', School of Public Policy and Department of Criminology, University of Maryland. Disponible en: http://jec.senate.gov/index.cfm?FuseAction=Files.View&FileStore_id=712e7919–ea4e–4ead–b770–c9b656e531d8 [ Links ]
16. UNITED NATIONS OFFICE ON DRUGS AND CRIME UNODC (2000 and 2004– 2009). World Drug Report. [ Links ]
17. UNITED NATIONS OFFICE ON DRUGS AND CRIME UNODC (1999 to 2003). Global Illicit Drug Trends. [ Links ]
18. UNITED NATIONS OFFICE ON DRUGS AND CRIME UNODC (2009a). Colombia, Monitoreo de Cultivos de Coca, june. [ Links ]
Primera versión recibida en agosto de 2009; versión final aceptada en noviembre de 2009